こんばんは。
引き続きゼロからディープラーニングを勉強してみる第5弾として、今回はSONY Neural Network Console から重みやバイアス値をエクスポートしてExcelに取り込んでみたり、ConvolutionとDepthwise Convolutionを比較してみたり、正答率を上げるためにニューロンを増やしたり、いろいろ実験したことを紹介します。
今回の実験で、ディープラーニングをマイコンや他ソフトへ実践するための道筋が出来た気がします。
学習済みニューラルネットワークから重み(W)とバイアス(b)を抽出できれば、そのままマイコンに取り込んで計算させることができるというわけです。
そして、ニューラルネットワークのニューロン(ノード)数を増やすと、中間層のConvolutionの重みパラメータ数が激増して、計算コストが増えることが分かりました。
非力なマイコンに取り込む場合、この計算コストを減らす工夫をして、その上で評価の正答率を上げなければならないということが良くわかりました。
このことは、SONYのNeural Network Consoleだけやっていただけでは理解できなくて、Excelに落とし込んで初めて理解できたんです。
ということで、これから今回の実験を紹介したいと思います。
この記事から見る方々は何をやっているか分からないと思いますので、過去4回シリーズの記事も参照してみてください。
●ゼロからディープラーニングを勉強してみる ~Excel編その1。自己流計算式の限界とバイアス、シグモイド関数について~
●ゼロからディープラーニングを勉強してみる ~Excel編その2。ニューラルネットワークと学習~
●ゼロからディープラーニングを勉強してみる ~Excel編その3。畳み込みニューラルネットワーク~
●ゼロからディープラーニングを勉強してみる ~その4。SONY Neural Network Console 導入編~
因みに、何度も言っておりますが、私はこの分野のド素人です。
何か間違えていたらコメント投稿等でご連絡いただけると助かります。
- 重みとバイアスをエクスポートする
- ConvolutionとDepthwise Convolutionについて
- Depthwise Convolutionを使ってニューラルネットワークを組んでみる
- Excelで作った畳み込みニューラルネットワークにパラメータを取り込んで評価を比較してみる
- 正答率を上げる実験
- まとめ
【目次】
1.重みとバイアスをエクスポートする
では、前回のNeural Network Console 導入編で手書き数字MNISTデータセットの学習が済んだので、このネットワークから重み(W)とバイアス(b)を取り出してみたいと思います。それができれば、ESP32やM5Stack、ラズパイなどの組み込みマイコンや、他のアプリで動作させることができます。
実は、これはNeural Network Console の操作方法としてはかなりややこしかったです。
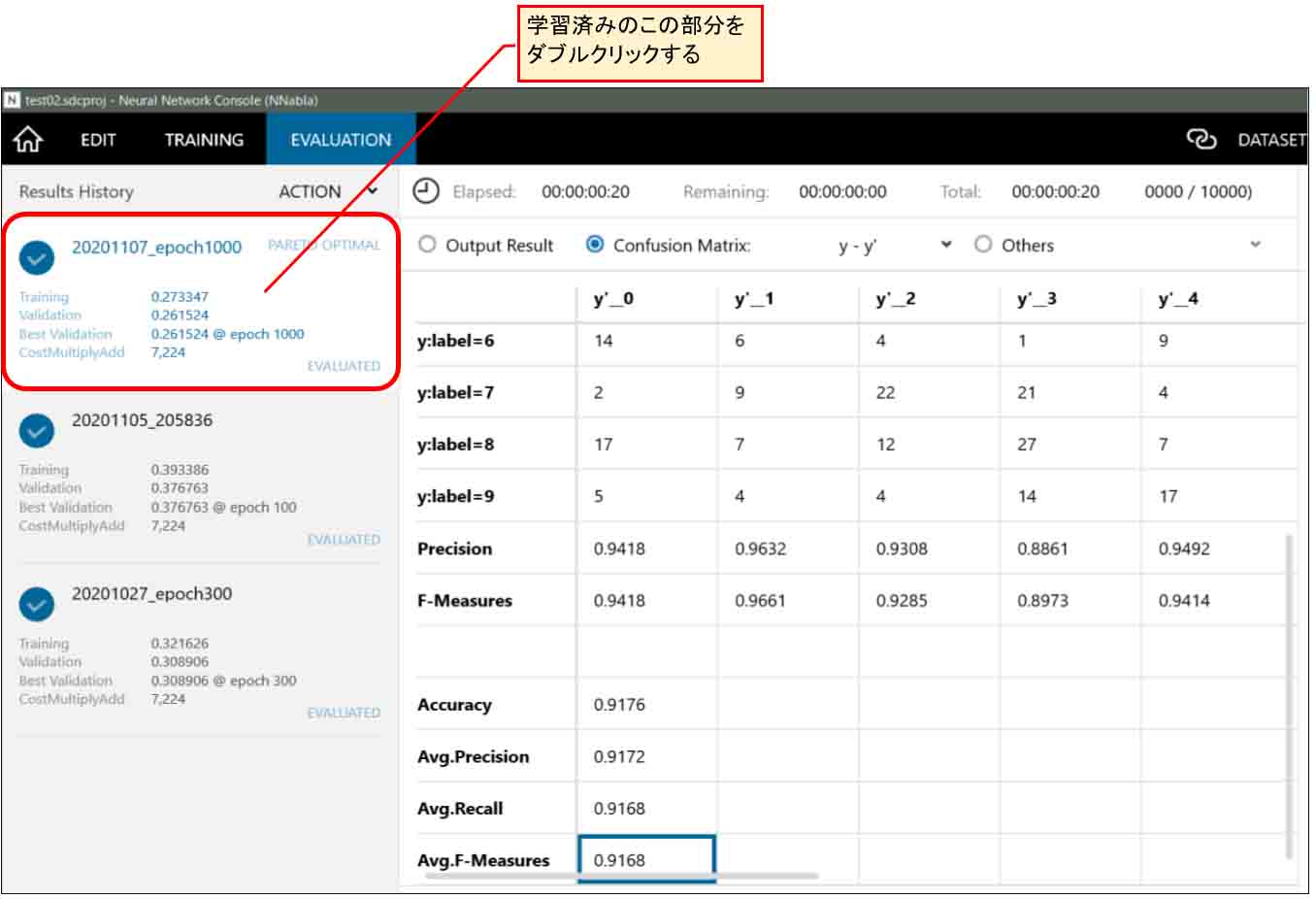
まず、下図の様にEVALUATIONタブまたはTRAININGタブのところで、左側の学習済みのファイルをダブルクリックします。
(図01-01)
すると、下図の様にエクスプローラーウィンドウが表示されます。
そこには学習済みのファイル群が格納されています。
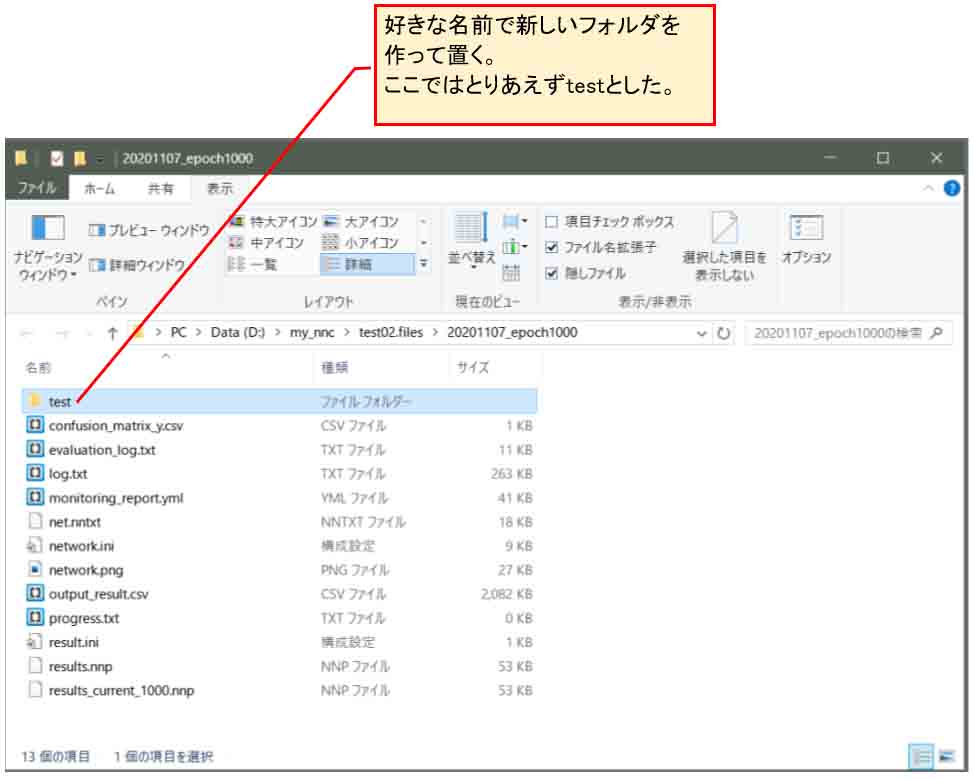
そして、そこに好きな名前で新しいフォルダを作って置きます。
ここでは「test」というフォルダにしました。
(図01-02)
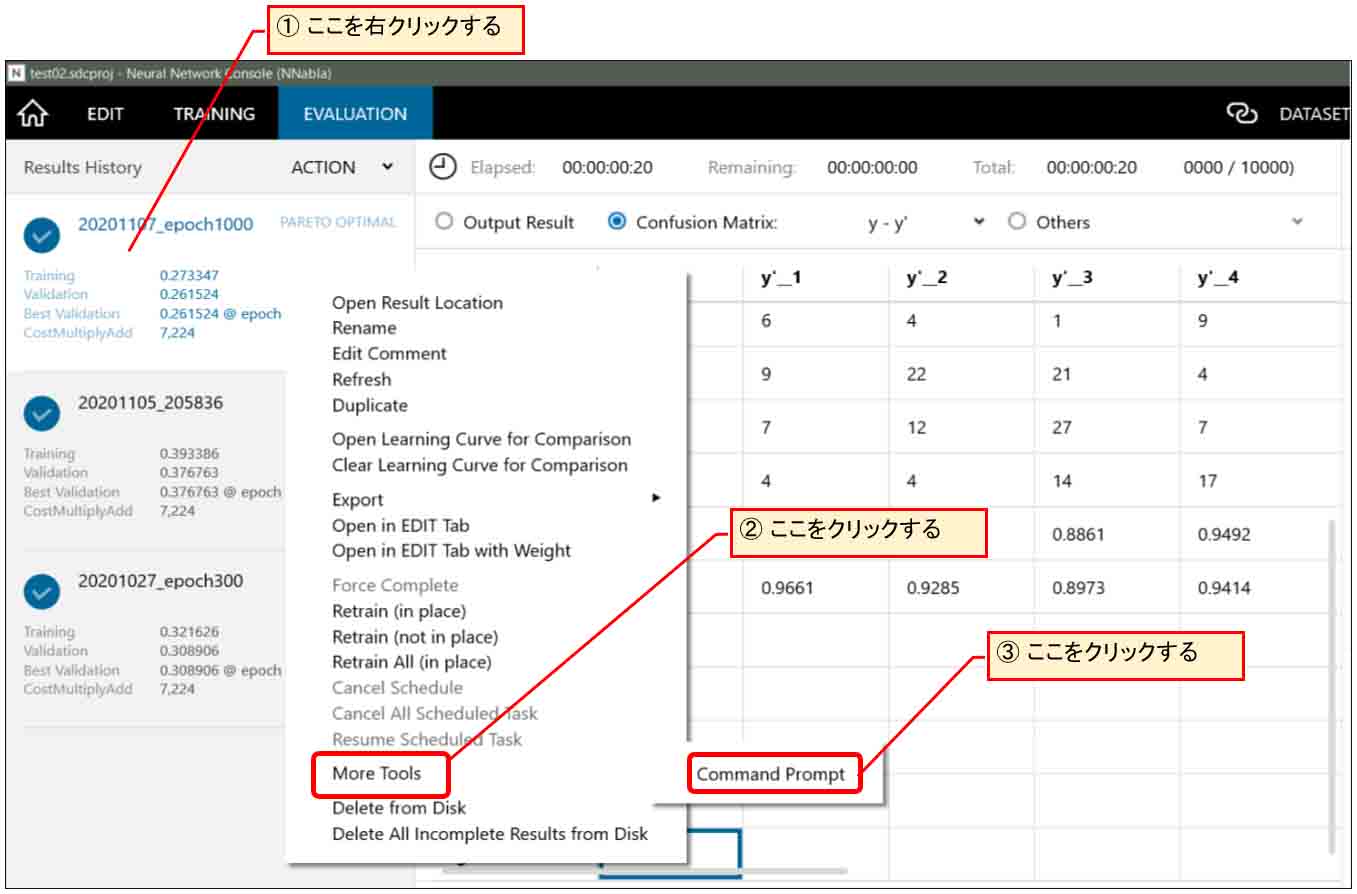
次に、下図の様に先ほどの左欄のファイルの所を右クリックすると下図の様にツール群メニューが現れるので、「More Tools」をクリックすると、「Command Prompt」という表示が出るので、そこをクリックします。
(図01-03)
すると、下図の様にWindows コマンドプロンプトが表示されます。
(図01-04)
ここからは、Pythonというディープラーニングでは主流で使われているプログラミング言語の関連ツールをインストールするコマンドを打つことになります。
因みに、Neural Network Console をインストールしたら、自動的にある程度Python関連がインストールされているようです。
では、次のコマンドを入力します。
nnabla_cli -h
nnblaとは、Pythonを用いたSONY製のNeural Networkライブラリだそうです。
cliはそのコマンドラインインターフェースを意味します。
そのヘルプを見ようとしています。
(図01-05)
そして、エンターキーを押すと、私の場合、以下の様なエラーが出ました。
この場合は、異常なので、 nnabla一旦アンインストールして、再インストールすると良いらしいです。
では、nnablaをアンインストールするために、まず、以下のコマンドを入力します。
pip uninstall -y nnabla
pipとはPythonパッケージをインストールするためのユーティリティコマンドだそうです。
そして、エンターキーを押すと以下のようにアンインストールできます。
(図01-06)
次に、nnblaを再インストールするために、以下のコマンドを入力します。
pip install --use-feature=2020-resolver nnabla
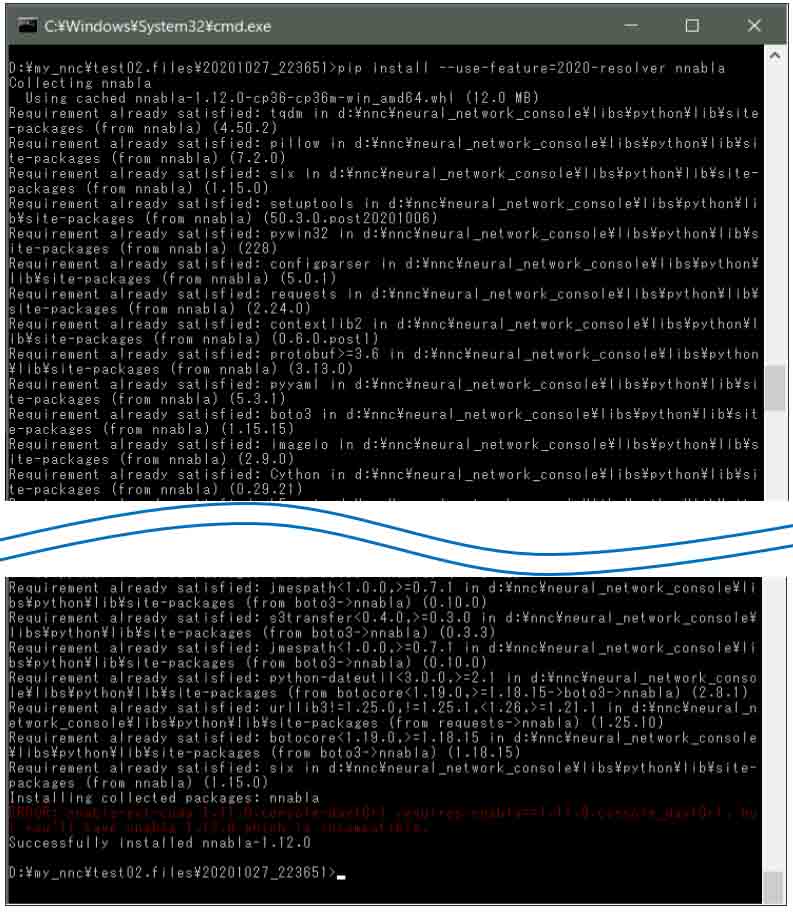
そして、エンターキーを押すと以下のように再インストールされます。
(図01-07)
ただ、赤い文字のエラーが出たので気になります。
こんなメッセージです。
これを日本語に訳すと
cudaという単語は、パソコンに積んであるNVIDIA製GPUのC/C++プログラミングモデルらしいです。
正直言って私には良くわからないのでこのメッセージは無視しました。
では、再度、以下のコマンドを打って、nnablaコマンドラインインターフェースにエラーが出ないか確かめます。
nnabla_cli -h
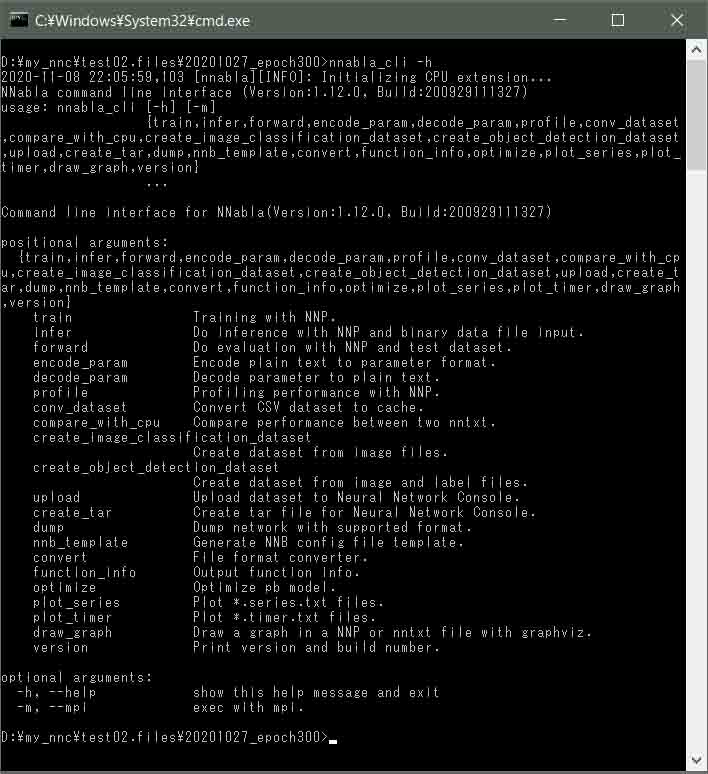
すると、下図の様に表示されればOKです。
(図01-08)
これでnnabla_cliコマンドが正常に動くようになりました。
そして、重み(W)とバイアス(b)のパラメータをエクスポートする準備が整いました。
では、(図01-02)で表示させたフォルダに存在する results.nnpというファイルから、重みとバイアス値をエクスポートします。
先ほど作成したtestフォルダに出力するようにします。
以下のコマンドを入力します。
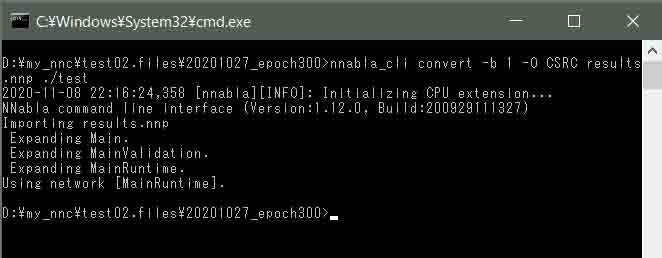
nnabla_cli convert -b 1 -O CSRC results.nnp ./test
そして、エンターキーを押すと以下のように表示されればOKです。
(図01-09)
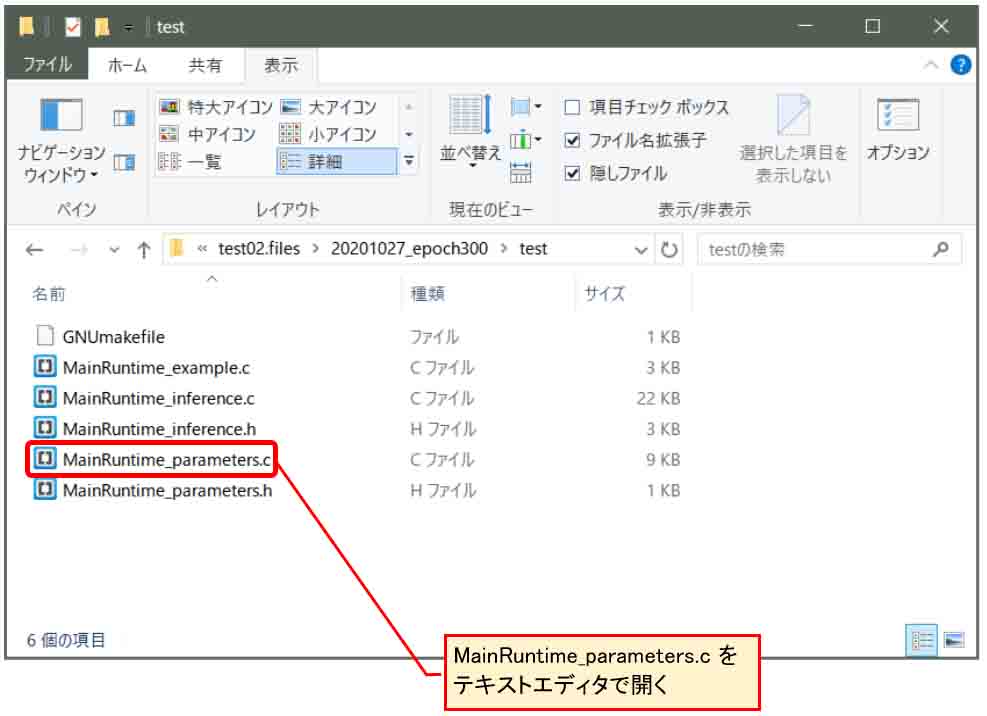
すると、先ほど作ったtestフォルダ内には以下の様なファイルがエクスポートされていると思います。
(図01-10)
これを見ると、Arduinoプログラミングをしている人にはお馴染みのC言語ファイルとヘッダが作成されていることが分かると思います。
これは、ESP32やM5Stack、ラズパイなどにも流用できそうです。
では、そのMainRuntime_parameters.c というファイルをメモ帳などのテキストエディタで開いてみます。
すると、こんな感じです。
(図01-11)
このように重み(W)がfloat型の配列で出力されていました。
そのままArduinoプログラミングに生かせそうですね。
では、MainRuntime_parameters.c の中にある重みとバイアスの個数を数えてみます。
こんな感じです。
Convolution 重み(W) : 48個
バイアス(b) : 3個
Convolution_2 重み(W) : 81個
バイアス(b) : 3個
Affine 重み(W) : 120個
バイアス(b) : 10個
あれれ??
Convolution_2 の重みの個数がやけに多いぞ?
重み(W)個数 + バイアス(b)個数 = 84
となっています。
前々回の8章では、2つ目の畳み込み層のパラメータ数は、
重み(W)個数 + バイアス(b)個数 = 30
のはずで、何かがおかしいぞ?
これでは、前々回8章のExcelニューラルネットワークに重みとバイアスを入れ込めません。
実は、この原因は、前々回記事の2回目のConvolutionが通常の物と異なり、Depthwise Convolutionというものだったことが分かりました。
これについては次の章で詳しく説明します。
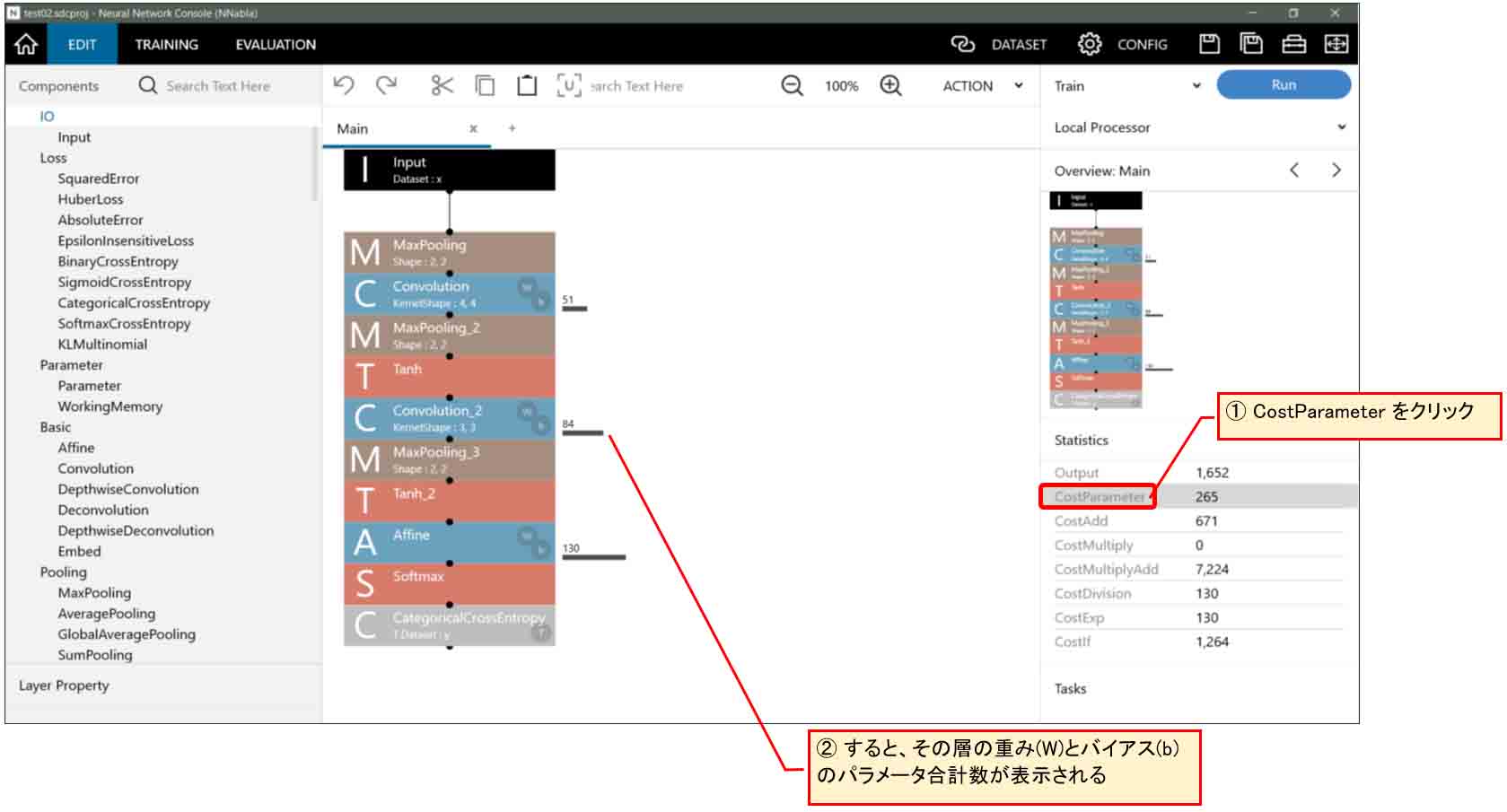
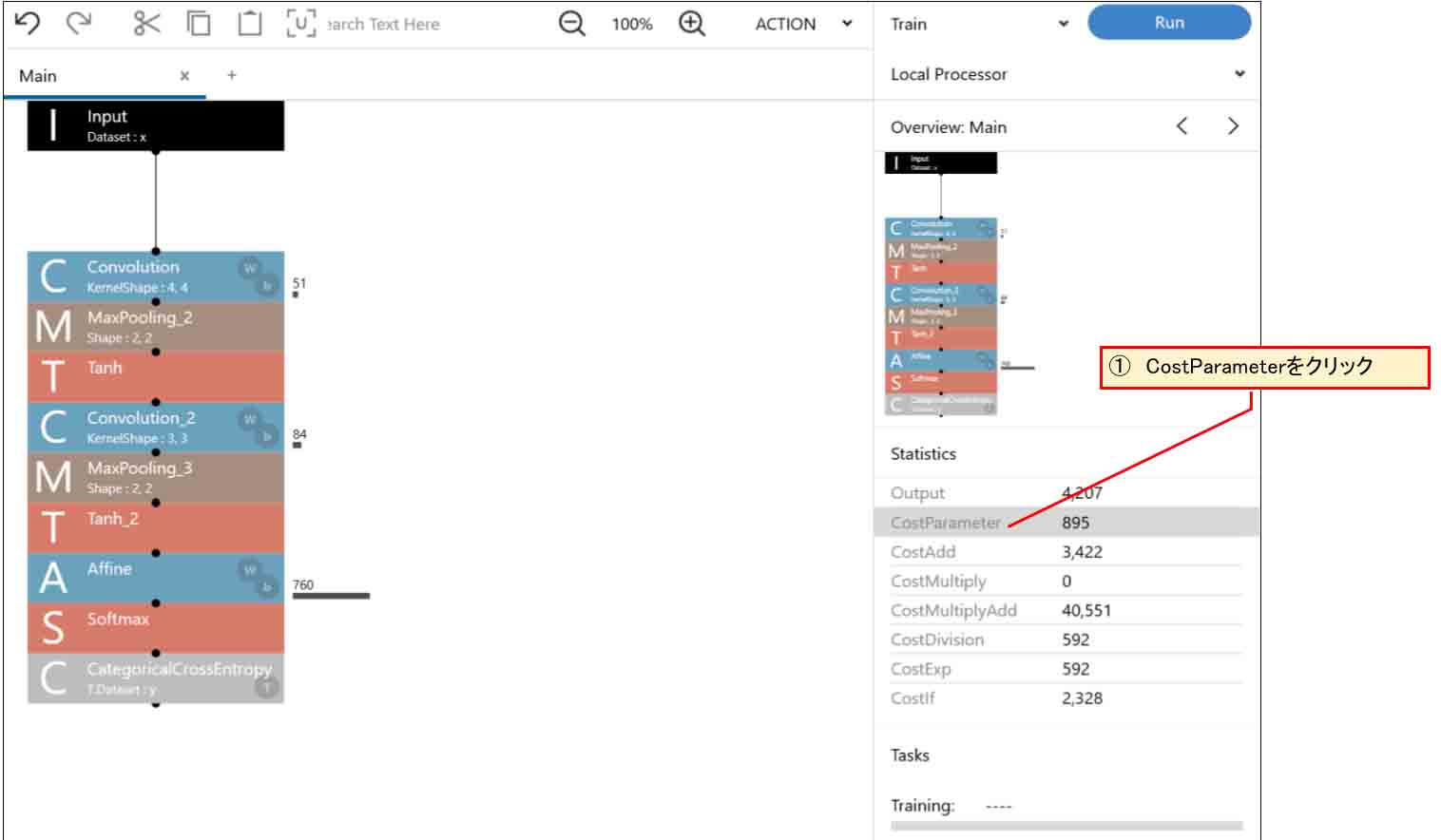
ところで、わざわざパラメータをエクスポートして重みとバイアスの個数を数えなくても、下図の様に、Neural Network Console上の右側のStatistics欄の「CostParameter」をクリックすれば、各層の重み(W)とバイアス(b)の合計値を表示してくれるという便利な機能がありました。
(図01-12)
これは良くできていますね。
さすが、SONY!
さて、先ほどからCostという用語が出現していますが、なんでコストなの? と思いませんか?
Deep Learning界隈では一般的に重みやバイアスの個数をコストと言うらしいです。
これはあくまで私の想像ですが、その個数が計算にかかるコスト(価値、損失)を示しているのだと思われます。
つまり、このコストが多いほど計算時間を浪費するため、コストはできるだけ少なくした方が良いと言えます。
生産現場と同じニュアンスみたいですね。
Arduino などの非力なマイコンに組み込む際にも、このコストは少ない方が断然良いですね。
2.ConvolutionとDepthwise Convolutionについて
さて、前章の重みパラメータ個数を数えて判明したのが、前々回記事の2回目のConvolutionは、通常のConvolutionとは異なるということでした。
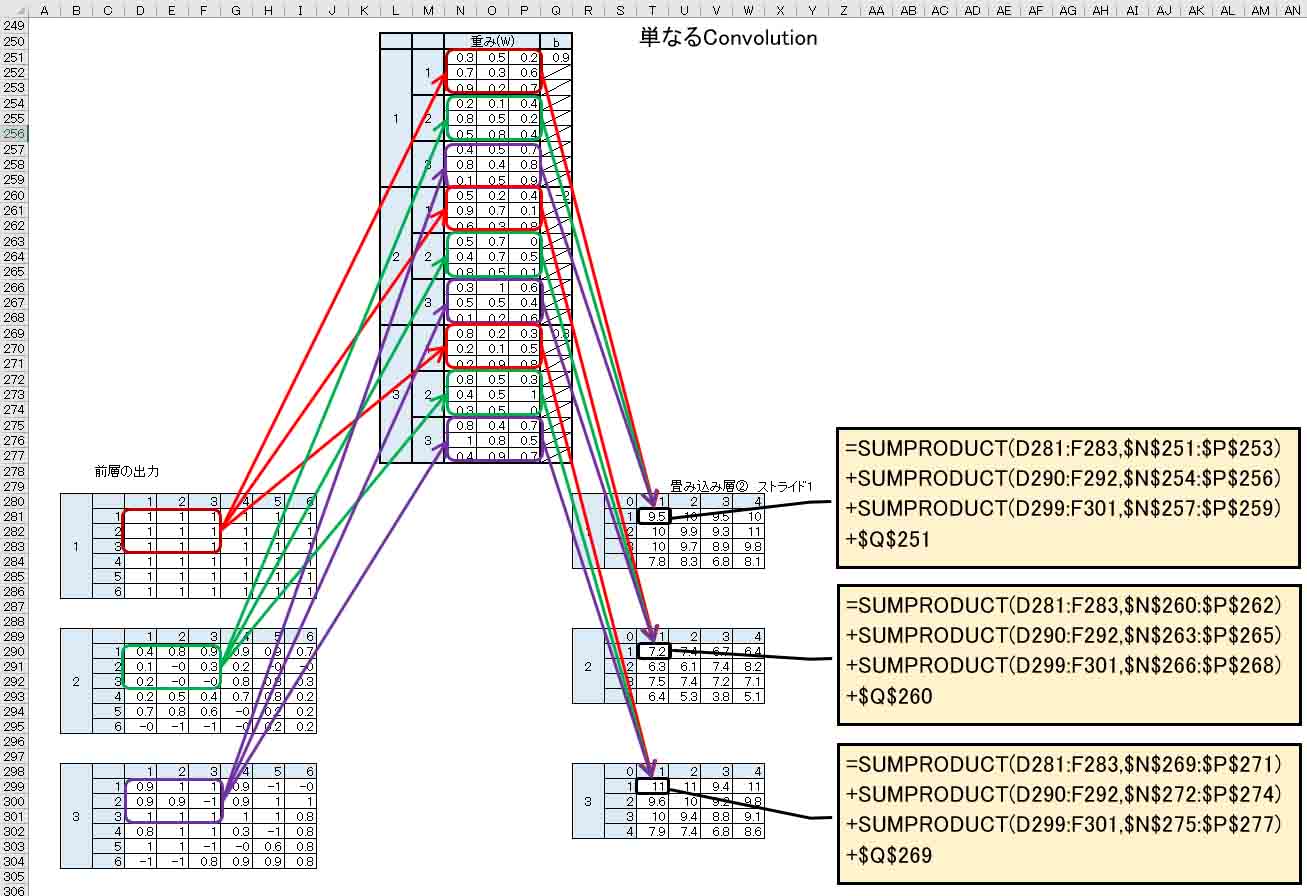
前々回記事8章の2つ目のConvolutionを抜粋して見てみると、前の層のニューロンから、重みフィルター3×3マスで畳み込んで、そのノードにだけ出力していました。
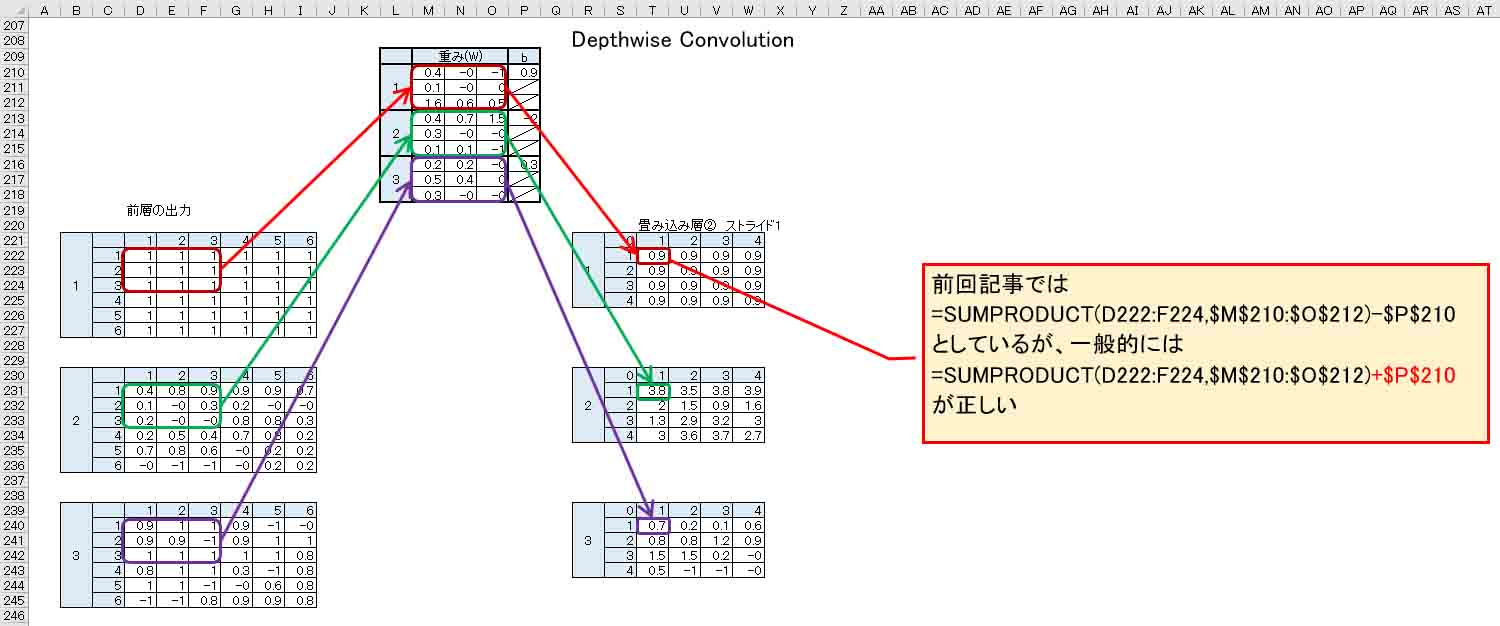
要するにExcel表にすると下図の様になるわけです。
(図02-01)
これは完全なConvolutionではなく、Depthwise Convolution と言うらしいです。
Depth-width ではないですよ! Depth-wiseです。
wise は「賢い」という意味の形容詞だそうですが、単語に-wiseが付くと、「~的な」とか「~について」という意味になるそうです。
つまり、Depthwise Convolutionは「深さについての畳み込み」「深さ方向の畳み込み」ということだそうです。
(正直、私は良くわかっていないので間違えていたらコメント投稿で教えてください。)
そして、もう一つ気付いた事ですが、前々回記事のExcelでは全てバイアスパラメータを数式中で減算していました。
しかし、SONY Neural Network Consoleの内部では加算していたことが判明しました。
一般的なディープラーニングの入門書でも基本的にはバイアス(b)を加算しているので、やはりそちらが正解なのでしょう。
要するに、以前の記事のシグモイド関数とバイアスについて述べた記事にあるように、
y = (WX1+WX2+WX3+……) + (- b)
と考えれば、加算しても同じ意味合いです。
ただ、学習後に最適化される重み(W)とバイアス(b)のパラメータの値は、加算と減算で大きく変わるので注意です。
ということで、今後は「バイアスは加算すべし」ということを頭の中に入れておこうと思います。
これについては、後の4章でも説明します。
ならば、通常のConvolutionはどういう計算になるのかというと、下図の様になるとのことです。
(図02-02)
Depthwise Convolutionの重み(W)の個数より3倍に増えて、
3×3×3×3 = 81 個
となります。
これを見て分かる通り、3ノード入力のConvolutionで3ノード出力の場合、各要素を合算してバイアスを加算しています。
ここでちょっと疑問なのは、各要素を合算してしまうと、特徴フィルターがごちゃ混ぜになるのではないかと思ってしまいます。ここは理解し難いところです。
ですが、こう考えてみると良いかも知れません。
例えば、イメージセンサがRGBフルカラーだとすると、白色の文字ならばRed, Green, Blue の各色に分離された手書き文字データになります。
その3枚のデータは全く同じではなく、濃淡などにより微妙に数値が違っているデータになっているはずです。
出力判定は、色とは全く無関係で、0~9の文字を判定できれば良いとします。
そう! 出力が色とは全く無関係だというところがミソです。
赤色の数字だったとしても0~9の数値しか判定しません。青色の文字でも同じです。
そう考えると、Redの画素パターンとGreenの画素パターンとBlueの画素パターンそれぞれを合算して畳んだ方が、どんな色でも0~9の数値を判定できるということになり、納得できると思います。
すると、本来のConvolutionは(図02-02)の計算方法が正しいと理解できると思います。
実際、いろいろ調べてみると、通常のConvolutionの方が精度は上で、Depthwise Convolutionは計算量を減らしたい場合の対策に使うようです。
前々回のExcelの場合では、ソルバーの制約上、通常のConvolutionを使うのは無理だったので、結果的にDepthwise Convolutionを使うしか無かったということだったわけです。
3.Depthwise Convolutionを使ってニューラルネットワークを組んでみる
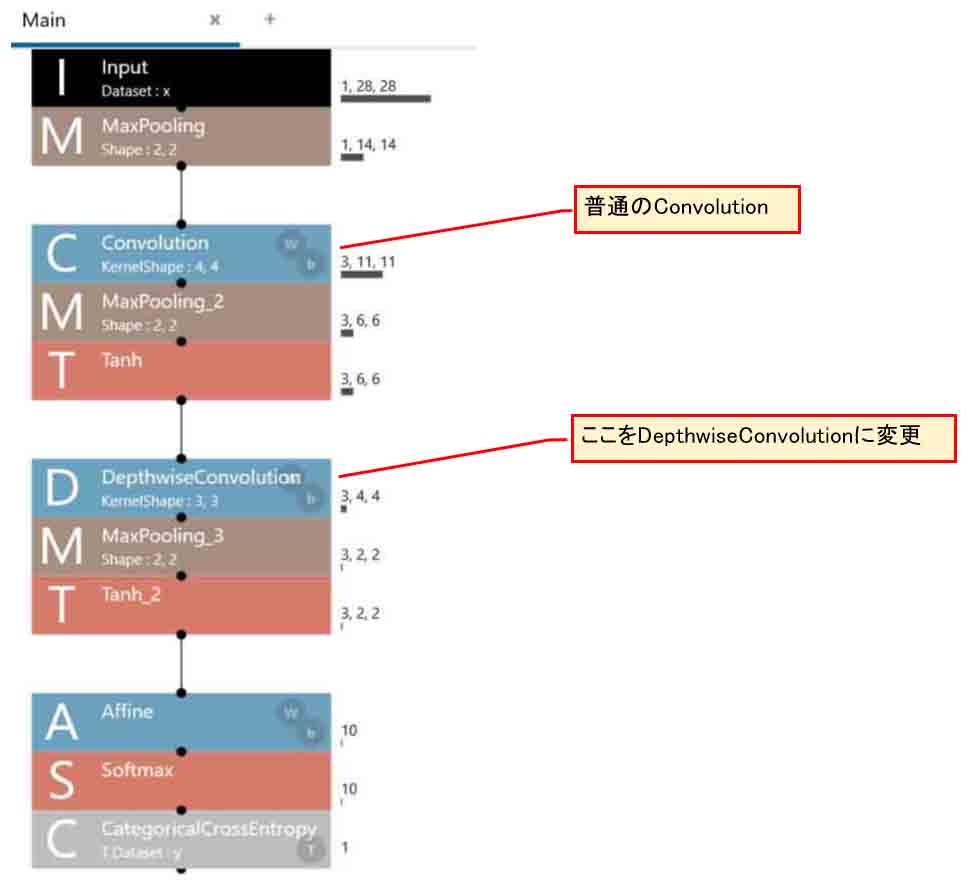
では、前々回8章のExcelニューラルネットワークの計算が合っているか確かめるために、前回記事4章の2つ目のConvolutionをDepthwise Convolutionに変えて組み直してみます。
こんな感じになります。
(図03-01)
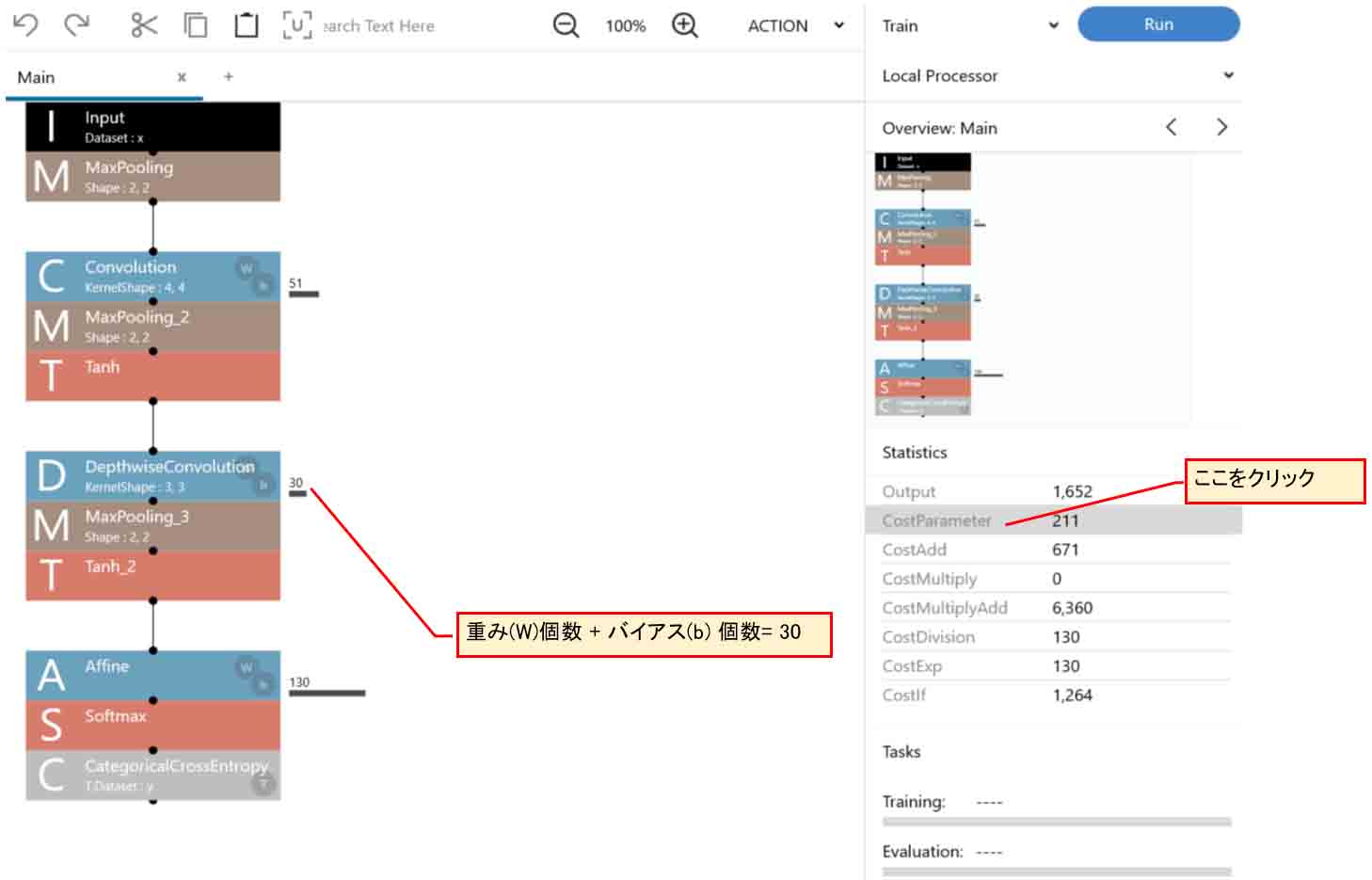
そして、CostParameterを見てみます。
こんな感じです。
(図03-02)
重み(W)個数 + バイアス(b)個数 = 30
となりましたね。
(図01-12)では84だったので、これで前々回記事8章のExcelネットワークと同じパラメータ個数になりました。
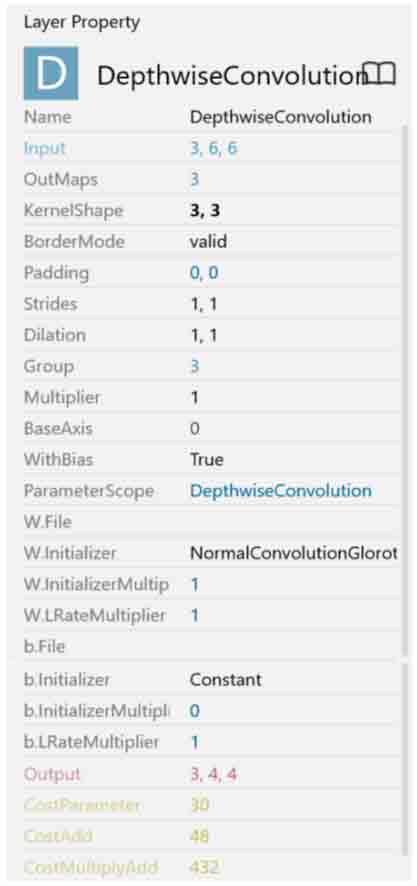
DepthwiseConvolutionのレイヤープロパティー設定はこんな感じです。
(図03-03)
前々回の8章と同じく、重みフィルター(KernelShape)は3×3とし、ストライドは1とすれば、Paddingは0で良いです。
では、これで「RUN」ボタンをクリックして学習させてみます。
「CONIFG」設定でMax Epoch は300にしました。
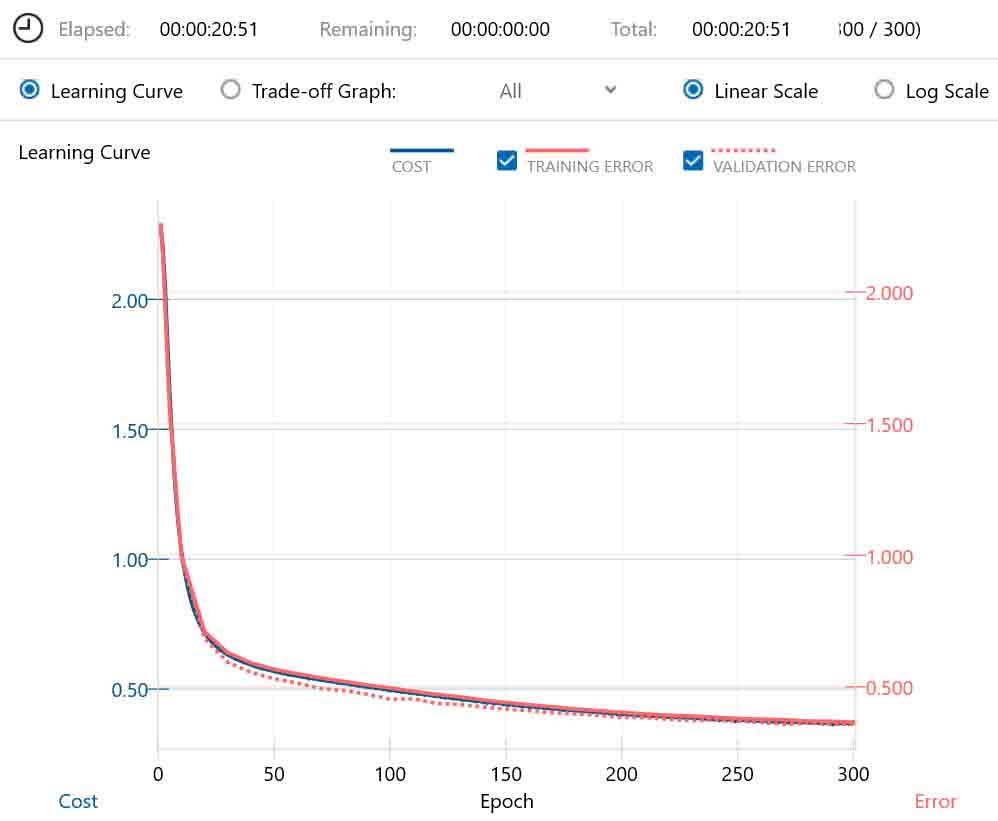
(図03-04)
計算時間は私の環境で20分51秒かかりました。
Costは0.37まで下がりましたが、この曲線を見る限りまだまだ値が下がりそうです。
この状態で「EVALUATION」タブを開いて、「Confusion Matrix」を選択して正答率を見てみると、以下のようになりました。
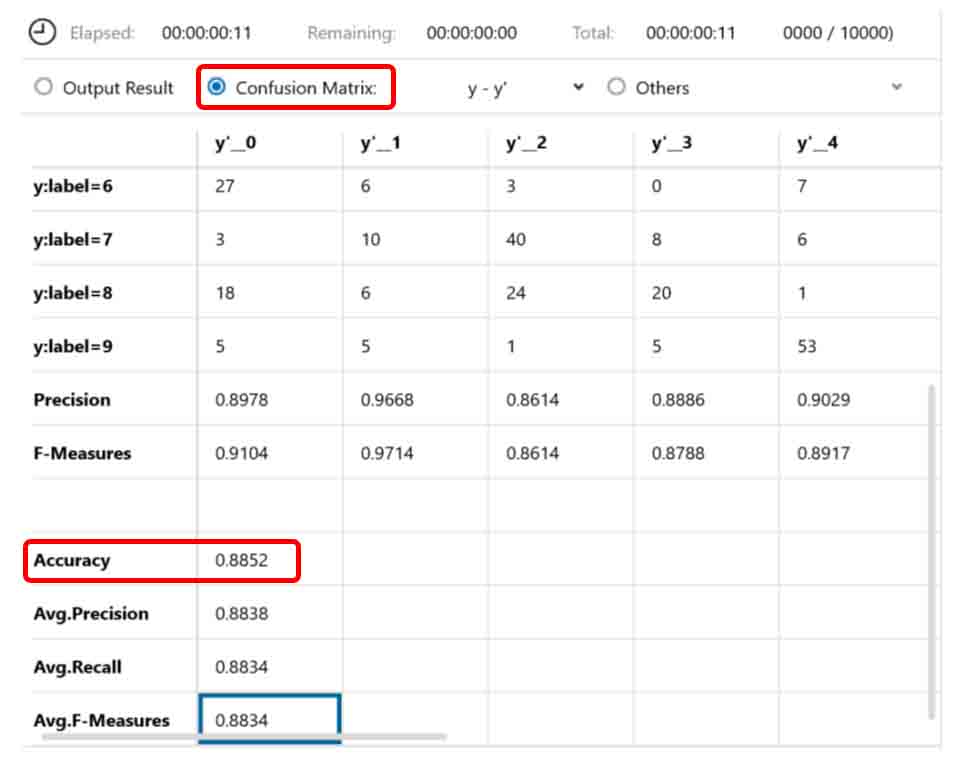
(図03-05)
Accuracy のところを見ると、正答率が0.88でした。これは低いですね。とても使えないデータです。
ただ、Max Epochの値を多くすれば、まだまだCostが下がるので、思い切って Max Epoch = 2000 にして、再度学習させてみます。
すると、こうなりました。
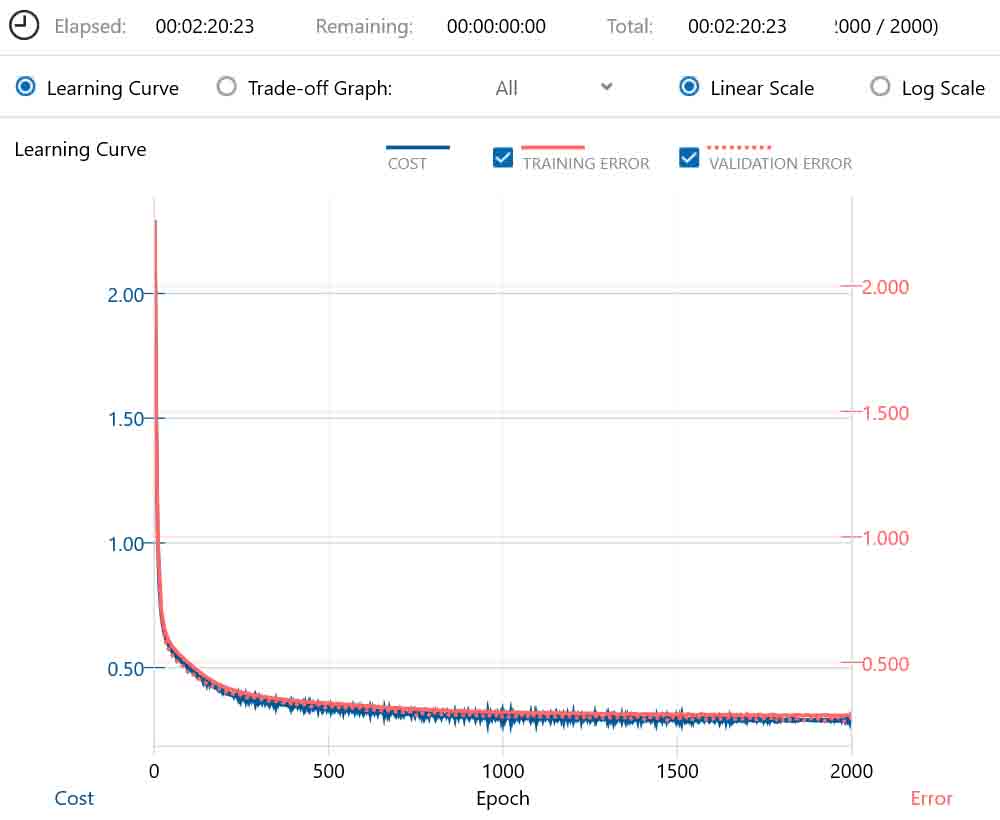
(図03-06)
計算時間は2時間20分もかかりました。
Costは0.288まで下がりました。
この曲線を見ると、最後の方はほぼ横這いでこれ以上学習回数を増やしても期待できませんね。
では、正答率を見てみます。
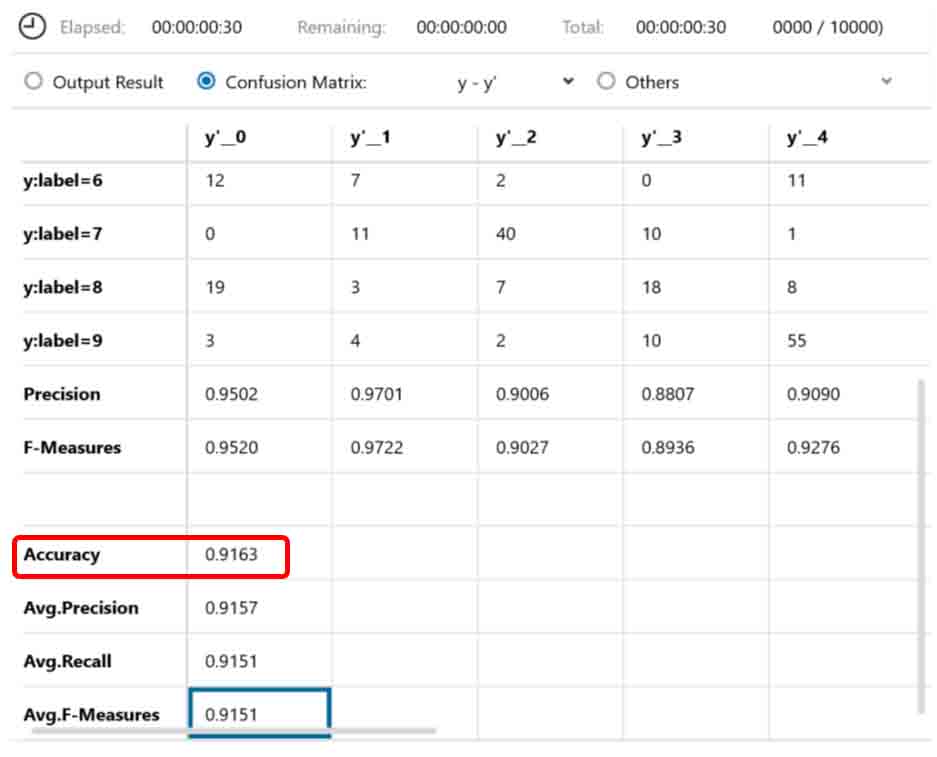
(図03-07)
やった!
正答率が0.916まで上がりました。
前々回の8章のExcelでの正答率が0.925なので、かなり近づきました。
ただ、実際の所、前々回の8章は学習データが903件の出力9ノードでしたが、今回の場合は学習データ60000件の出力10ノードです。
ですから単純に比較はできませんが、個人的にほぼ同じような結果になったと判断しちゃおうと思います。
4.Excelで作った畳み込みニューラルネットワークにパラメータを取り込んで評価を比較してみる
では、前章の学習結果で得た重みとバイアスのパラメータをエクスポートして、それを前々回の8章のExcel表に当てはめてみて、評価を比べてみたいと思います。
先の1章で紹介したように、エクスポートした重みとバイアスデータはMainRuntime_parameters.cファイルにテキスト形式で保存されています。
これをコピペしてエクセルに取り込むわけですが、データ1つずつコピペするのは骨が折れるし誤りの元です。
そこで、独自にマクロ等を使ってExcelに取り込む方法をやってみます。
まず、GitHubの以下のリンクに、Excelファイルをアップロードしてあるので、興味がある方はご自由にダウンロードして使って下さい。
https://github.com/mgo-tec/test_excel_deeplearning/blob/master/NNC/weight_bias_alignment.xlsx
weight_bias_alignment.xlsx
というファイルを使います。
これにはマクロはありません。
マクロ付きファイルをアップロードしてしまうと、ダウンロードする時にウィルスソフトで弾かれてしまうので、後に紹介するマクロコードを入力してください。
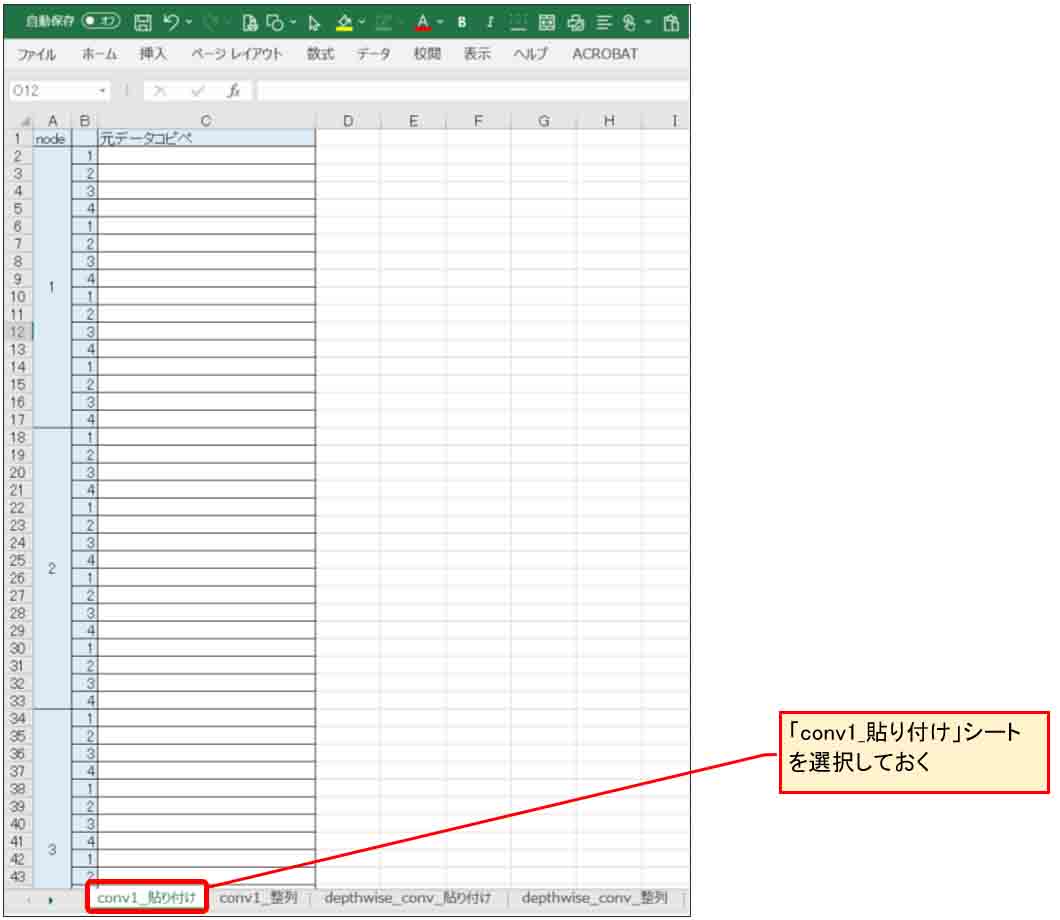
そのファイルを開いて、下図の様に「conv1_貼り付け」というシートを開いておきます。
(図04-01)
次に、先に紹介したエクスポートで生成された MainRuntime_parameters.cファイルをテキストエディタで開きます。
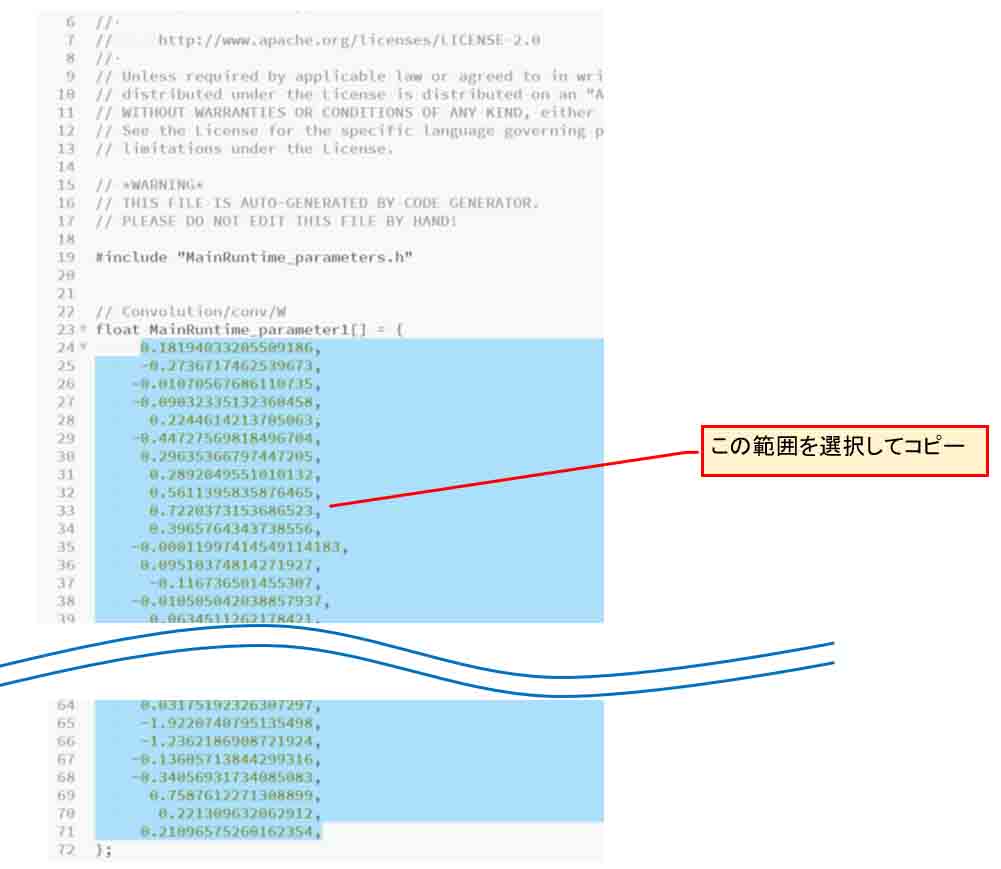
そして、下図の様に float MainRuntime_parameter1[] の配列のパラメータを選択します。
これは、Convolutionレイヤーの重み(W)です。
(図04-02)
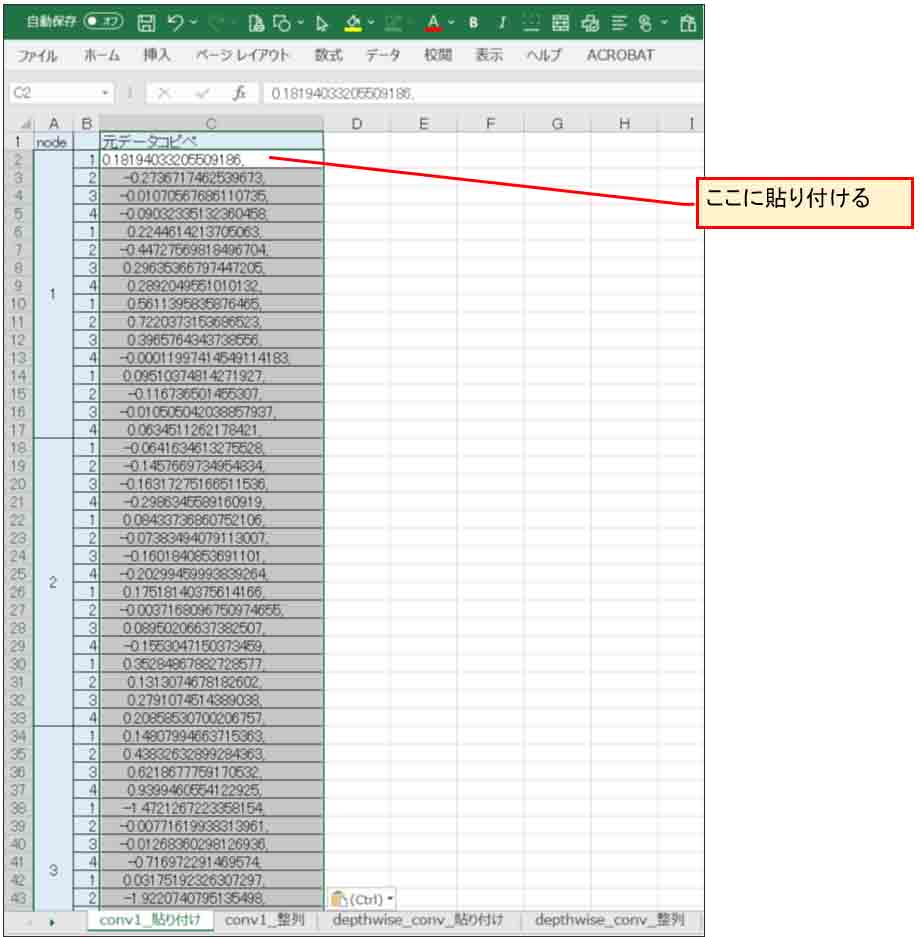
そうしたら、先ほどのExcelファイルの「conv1_貼り付け」シート上の数の位置にペースト(貼り付け)します。
(図04-03)
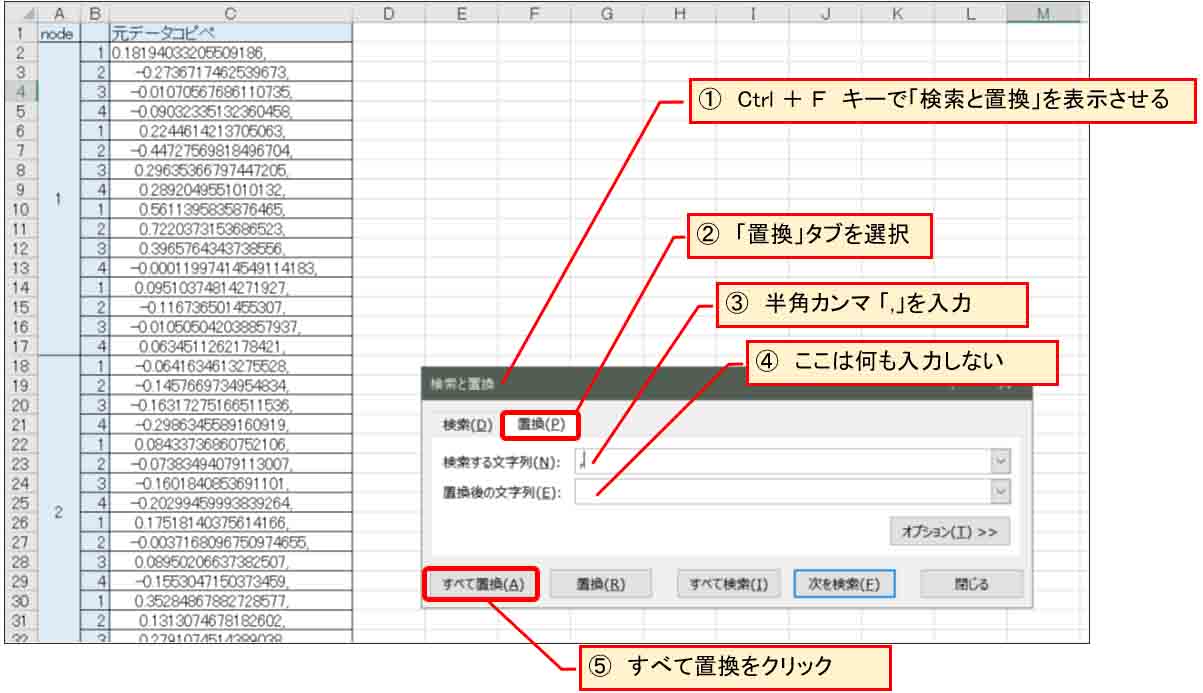
ただ、このままだと文字列データと認識されていて、カンマも入っているので、カンマを削除します。
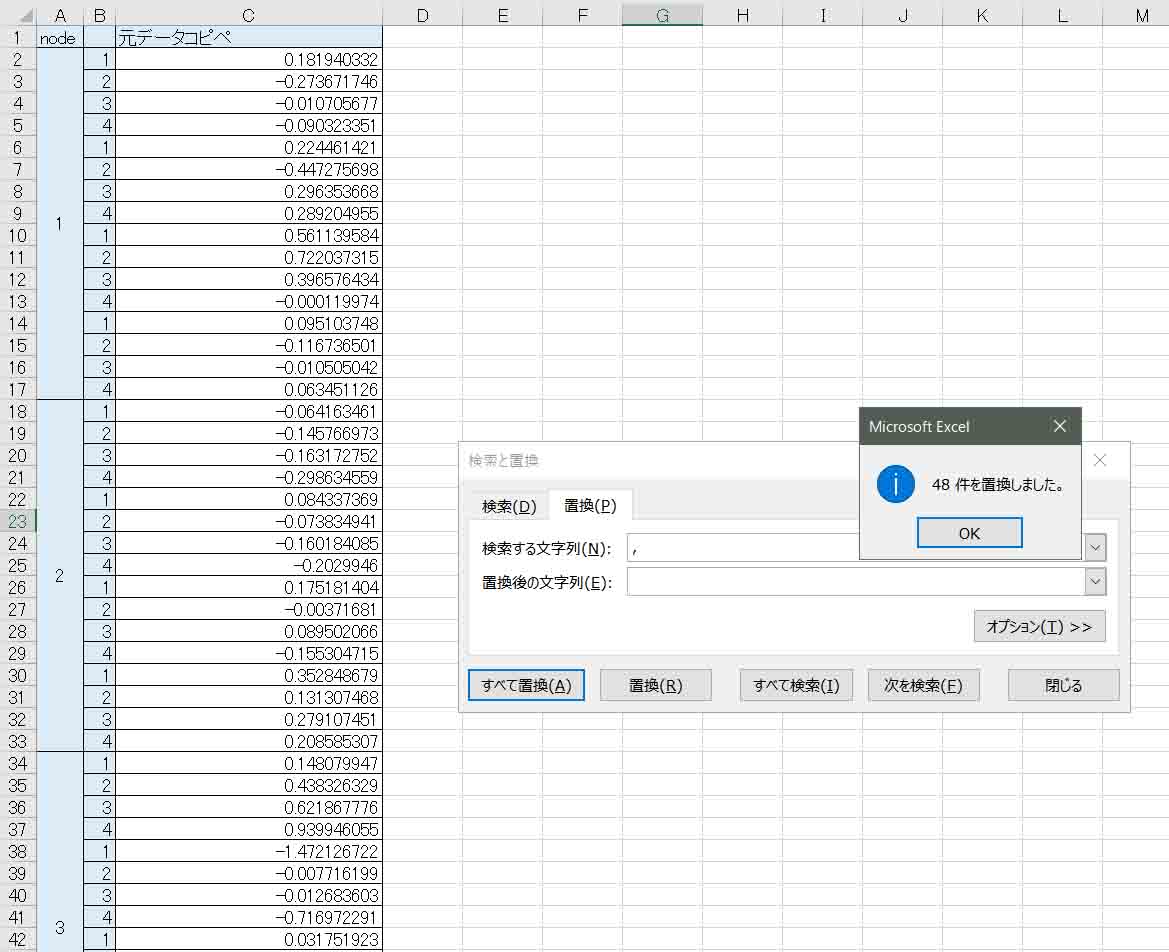
その場合、Ctrlキー+「F」キーを押して「置換」を用いて一括除去します。
下図の様な感じです。
(図04-04)
すると、下図の様に半角カンマが一括削除され、自動的に数値として表示されるようになります。
(図04-05)
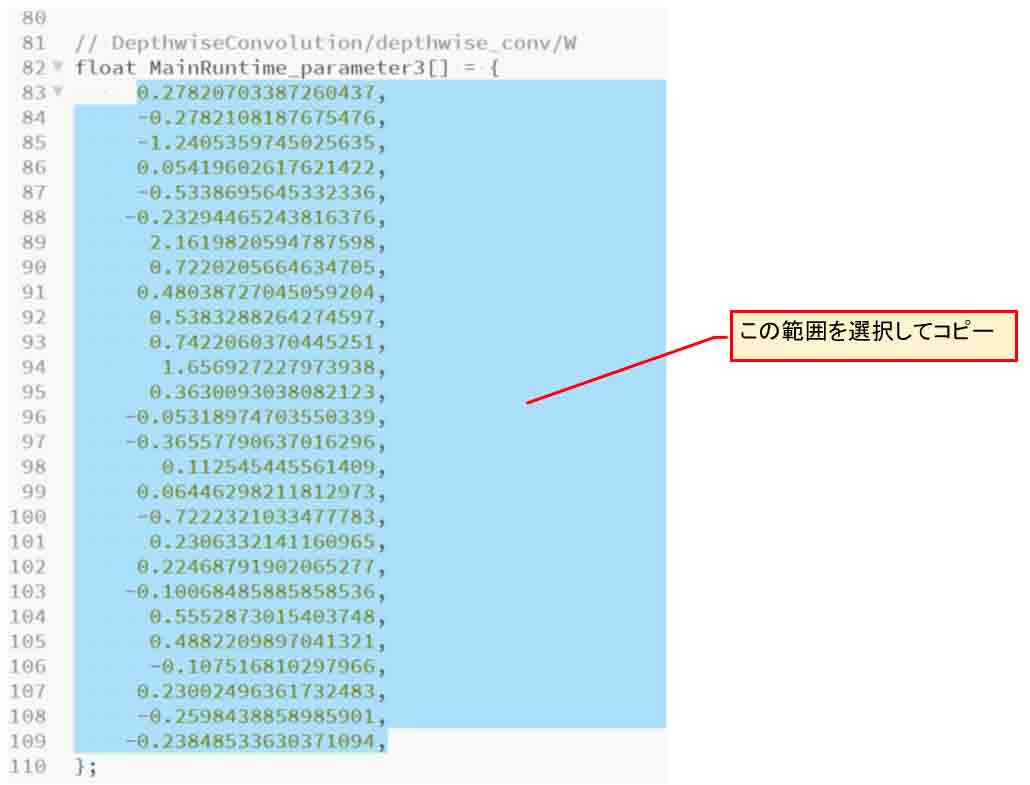
同じ様にfloat MainRuntime_parameter3[]のところ、つまり、Depthwise Convolutionの重み(W)をコピーします。
(図04-06)
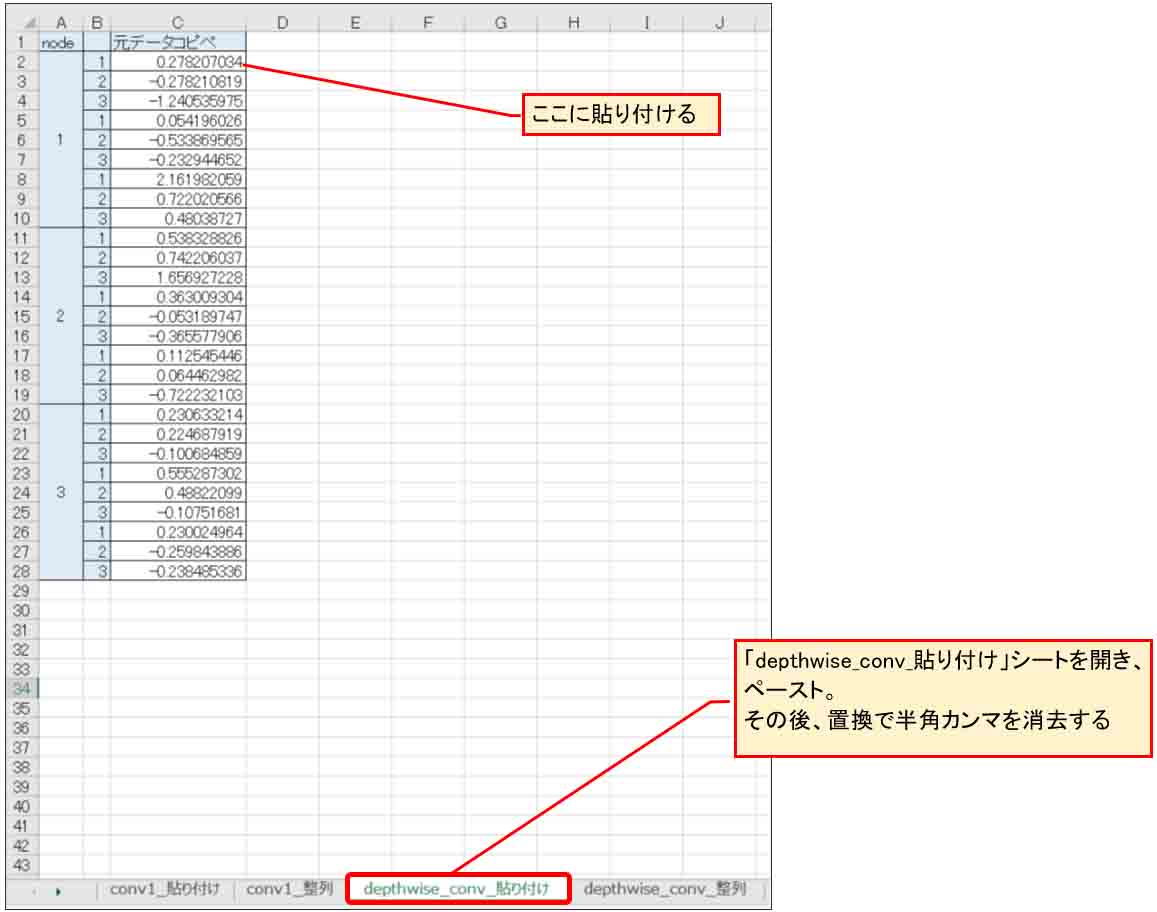
そしたら、今度は先ほどのExcelファイルの「depthwise_conv_貼り付け」シートを開き、下図の位置にペースト(貼り付け)して、同じように置換で半角カンマを消去します。
(図04-07)
次に、Affineレイヤーのfloat MainRuntime_parameter5[]のところの重み(W)をコピーします。
Affineの重みは120個もあり、これを一つ一つコピーするのは無理ですね。
(図04-08)
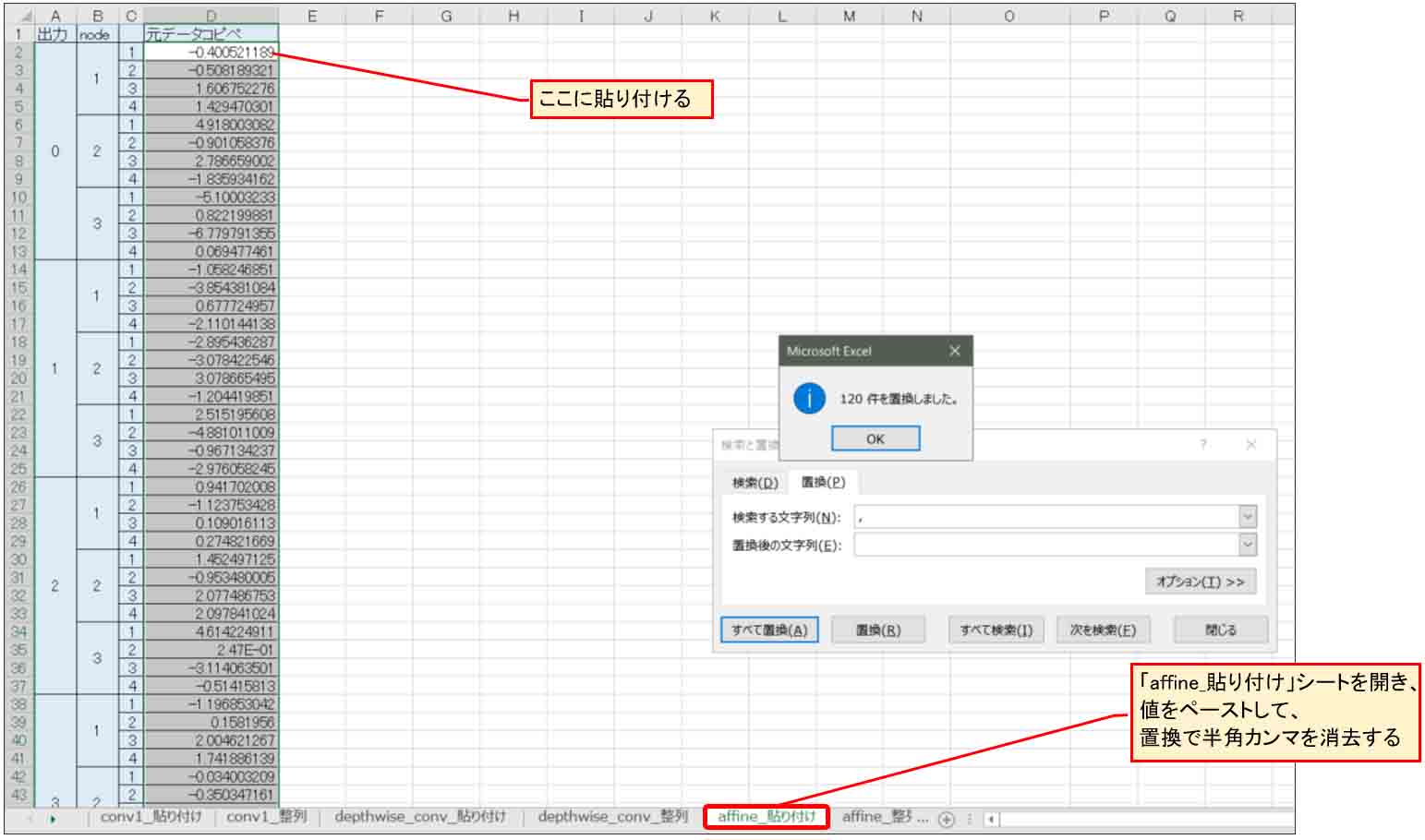
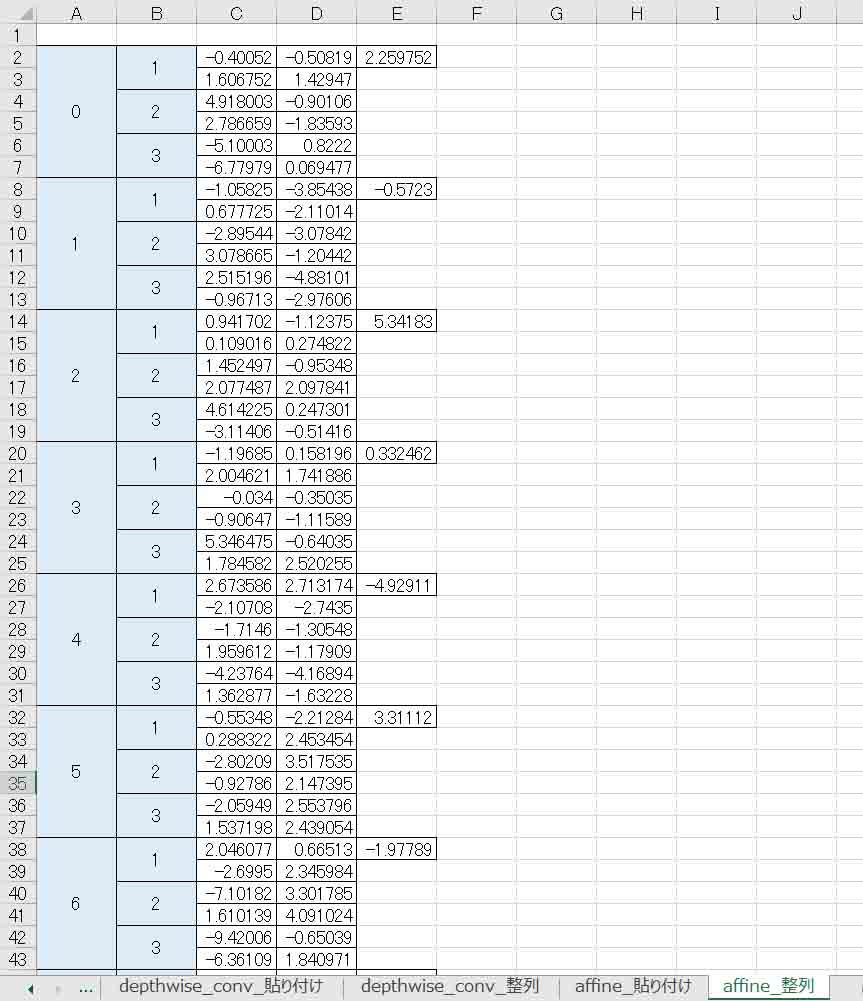
そうしたら、先ほどのExcelファイルの「Affine_貼り付け」シートを開き、同様に下図の位置にペーストして、置換で半角カンマを消去しておきます。
(図04-09)
バイアスについてのコピペは後で紹介します。
次に、このExcelファイルに新規マクロを作成します。
独自に作った以下のコードをマクロに入力して、実行させます。
素人コードなので、動作は保証しません。
Sub Weight()
Dim bytTmpData As Double
Dim i, j, k, ii As Long
Dim kk As Byte
Dim lngWeightXcel As Long
Dim lngWeightYcel As Long
Dim lngInputXcel As Long
Dim lngInputYcel As Long
Dim lngPixSize As Long
Dim lngMax As Long
Dim lngKernelSize As Long
Dim lngOutStartXcel As Long
Dim lngOutStartYcel As Long
Dim lngInputNodeNum As Long
Dim lngOutNodeNum As Long
Dim strSheetConv1 As String
Dim strSheetConv2 As String
Dim strSheetAffine As String
Dim strSheetConv1_out As String
Dim strSheetConv2_out As String
Dim strSheetAffine_out As String
'//シート名初期化
strSheetConv1 = "conv1_貼り付け"
strSheetConv2 = "depthwise_conv_貼り付け"
strSheetAffine = "affine_貼り付け"
strSheetConv1_out = "conv1_整列"
strSheetConv2_out = "depthwise_conv_整列"
strSheetAffine_out = "affine_整列"
'//convolution1 4x4 3node
lngKernelSize = 4
lngPixSize = lngKernelSize * lngKernelSize
lngInputXcel = 3
lngInputYcel = 2
bytTmpData = 0
lngOutStartXcel = 2
lngOutStartYcel = 2
lngOutNodeNum = 3
For k = 0 To lngOutNodeNum - 1
For j = 0 To lngKernelSize - 1
lngWeightYcel = lngOutStartYcel + j * 1
For i = 0 To lngKernelSize - 1
lngWeightXcel = lngOutStartXcel + i * 1
bytTmpData = Worksheets(strSheetConv1).Cells(lngInputYcel, lngInputXcel).Value
Worksheets(strSheetConv1_out).Cells(lngWeightYcel, lngWeightXcel).Value = bytTmpData
lngInputYcel = lngInputYcel + 1
Next i
Next j
lngOutStartYcel = lngWeightYcel + 1
Next k
'//Depthwise Convolution 3x3 3node
lngKernelSize = 3
lngPixSize = lngKernelSize * lngKernelSize
lngInputXcel = 3
lngInputYcel = 2
bytTmpData = 0
lngOutStartXcel = 2
lngOutStartYcel = 2
lngOutNodeNum = 3
For k = 0 To lngOutNodeNum - 1
For j = 0 To lngKernelSize - 1
lngWeightYcel = lngOutStartYcel + j * 1
For i = 0 To lngKernelSize - 1
lngWeightXcel = lngOutStartXcel + i * 1
bytTmpData = Worksheets(strSheetConv2).Cells(lngInputYcel, lngInputXcel).Value
Worksheets(strSheetConv2_out).Cells(lngWeightYcel, lngWeightXcel).Value = bytTmpData
lngInputYcel = lngInputYcel + 1
Next i
Next j
lngOutStartYcel = lngWeightYcel + 1
Next k
'//affine 2x2 10node 2out
lngKernelSize = 2
lngPixSize = lngKernelSize * lngKernelSize
lngInputXcel = 4
lngInputYcel = 2
bytTmpData = 0
lngOutStartXcel = 3
lngOutStartYcel = 2
lngInputNodeNum = 3
lngOutNodeNum = 10
For ii = 0 To lngOutNodeNum - 1
For k = 0 To lngInputNodeNum - 1
For j = 0 To lngKernelSize - 1
lngWeightYcel = lngOutStartYcel + j * 1
For i = 0 To lngKernelSize - 1
lngWeightXcel = lngOutStartXcel + i * 1
bytTmpData = Worksheets(strSheetAffine).Cells(lngInputYcel, lngInputXcel).Value
Worksheets(strSheetAffine_out).Cells(lngWeightYcel, lngWeightXcel).Value = bytTmpData
lngInputYcel = lngInputYcel + 1
Next i
Next j
lngOutStartYcel = lngWeightYcel + 1
Next k
lngOutStartYcel = lngWeightYcel + 1
Next ii
End Sub
すると、下図の様に、各「○○_整列」シートに重み(W)パラメータが整列されていると思います。
下図では、「conv1_貼り付け」シートの重み(W)パラメータが「conv1_整列」シートに再編成されています。
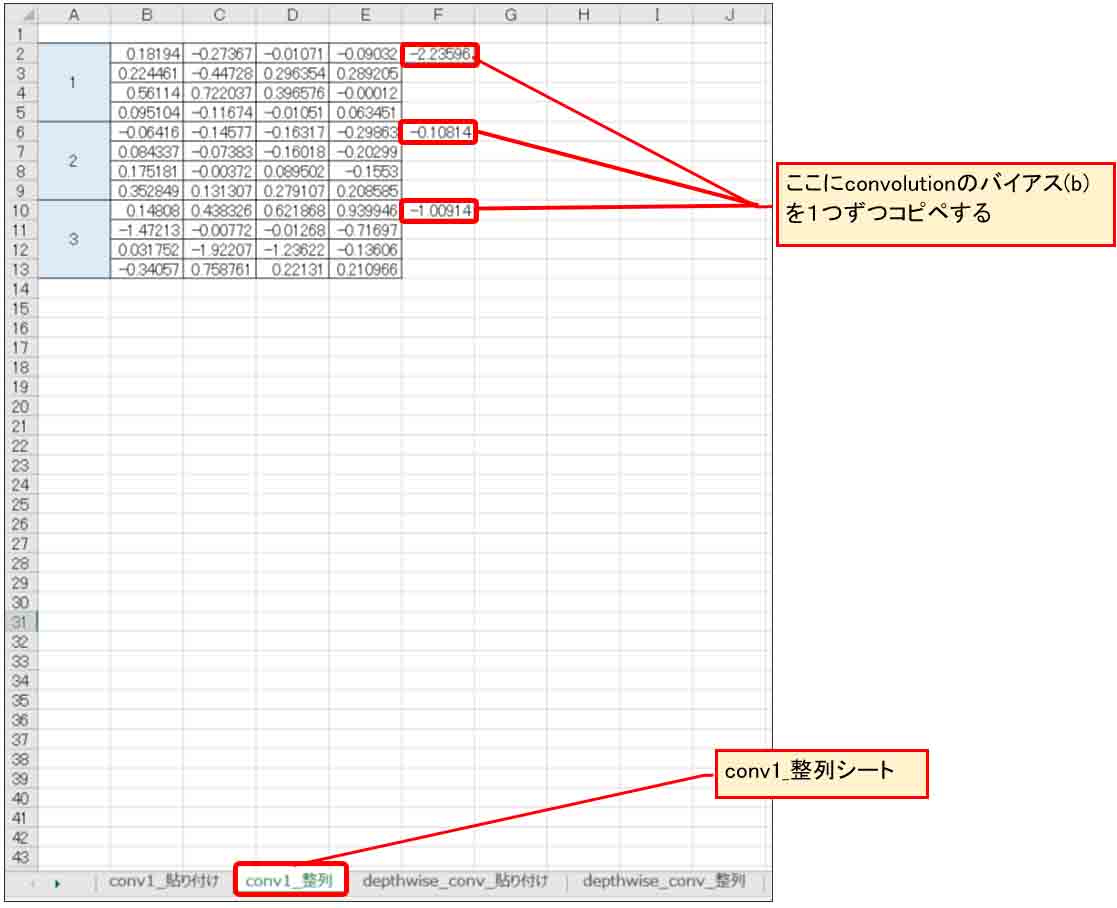
ただ、まだ重みパラメータしかないので、これからバイアスデータを1個ずつ下図の位置にコピペします。
(図04-10)
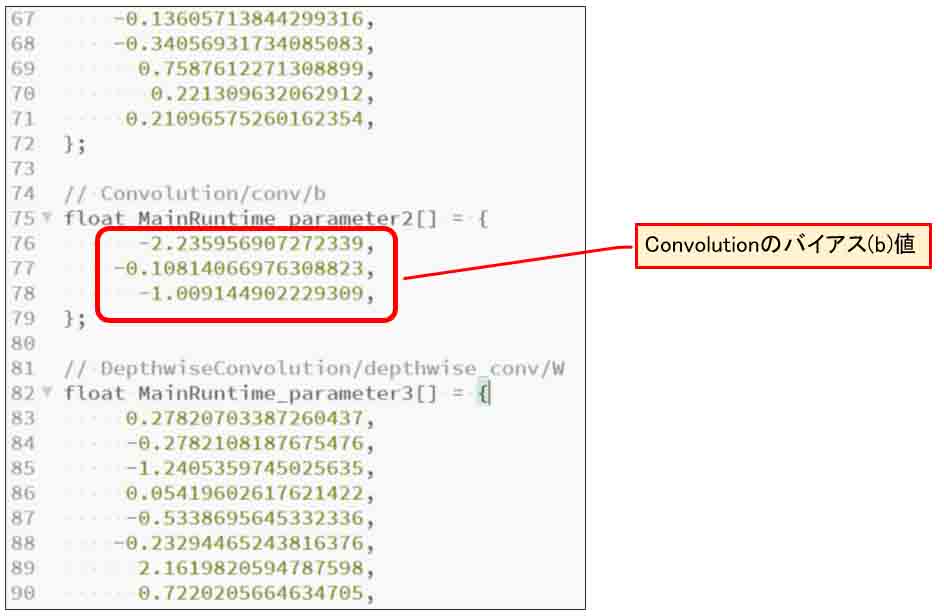
Convolutionレイヤーのバイアス(b)値は、float MainRuntime_parameter2[]のところにあります。
下図の様なところです。
(図04-11)
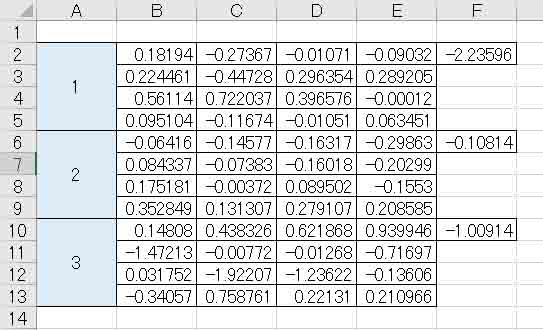
半角カンマを除いて一つずつコピペすると、以下のようになります。
(図04-12)
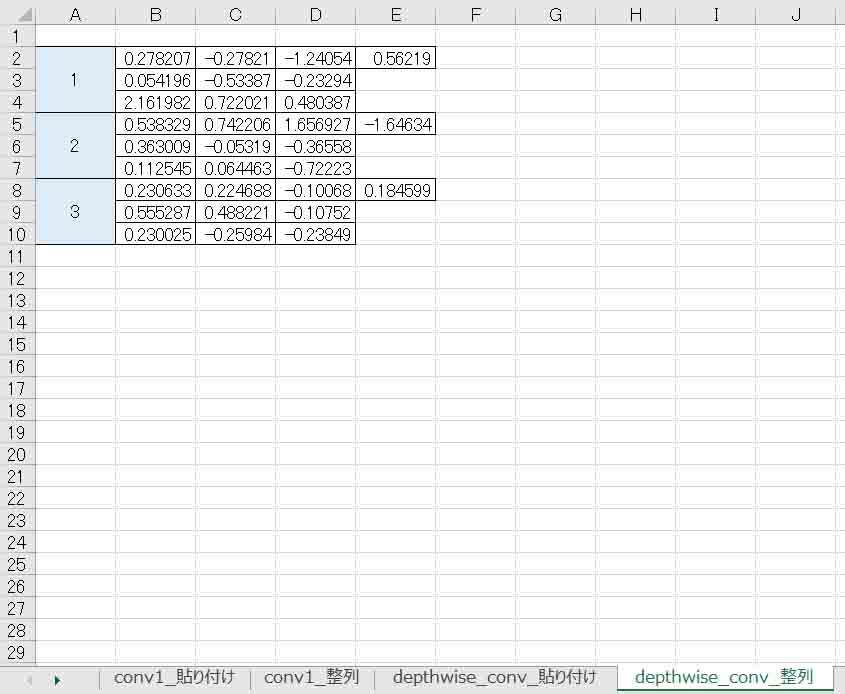
同じように、DepthwiseConvolutionレイヤーは「depthwise_conv_整列」シートに出力されているので、同様にfloat MainRuntime_parameter4[]のところのバイアスデータを1つずつコピペします。
(図04-13)
Affineレイヤーも同様にfloat MainRuntime_parameter6[]のところのバイアスデータを1つずつコピペします。
Affineレイヤーはバイアスが10個と数が多いので、事前に空欄の所にコピペして置換で半角カンマを除去すると良いと思います。
(図04-14)
以上で前々回8章のExcelのニューラルネットワークに重みとバイアスデータをコピペする準備ができました。
本当はバイアスデータも含め、マクロで一気に全て整列させるようにしたかったところですが、この1回くらいしか使わないので、マクロ自動化は重み(W)だけでやめときました。
では、前々回の8章のExcel畳み込みニューラルネットワークにこの重み(W)とバイアス(b)を入れ込んでみます。
上記の「conv1_整列」シートの重みとバイアスは前々回8章の畳み込み層①の重みとバイアスにコピペします。
「depthwise_conv_整列」シートの重みとバイアスは、畳み込み層②の重みとバイアスにコピペします。
そして、「affine_整列」シートの重みとバイアスは出力の所にコピペします。
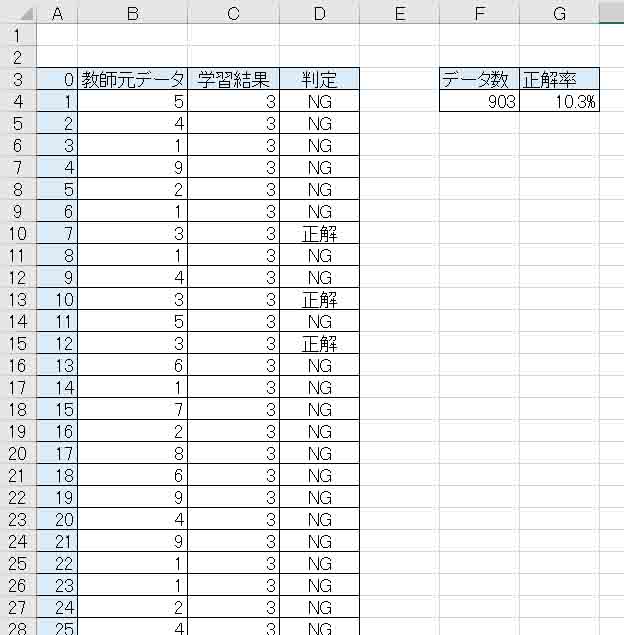
すると、前々回の8章の正答率は下図の様になりました。
(図04-15)
あれあれ?? おやおや???
正答率10%ってあまりにもおかしいですね。
どこがどう間違えてしまったんでしょうか?
この原因を突き止めるのに長い長い時間がかかりました。
何度も何度も学習させてはパラメータを変えたり、ネットワーク構造を変えたり、いろいろ試してみました。
SONYのNeural Network Consoleで調べても、レイヤーの計算方法はブラックボックスになっているので、Excelのどこが間違えているのか、さっぱり分かりませんでした。
そこで、かれこれ2週間くらい試行錯誤した結果、ようやく原因を突き止めました。
それは、2章でも述べましたが、バイアス(b)の計算方法を間違えていたのです。
前々回記事では畳み込みやAffineで重みとバイアスを計算する時、
y = (WX1+WX2+WX3+……) – b
としていました。つまり、
=SUMPRODUCT($BS$54:$BV$57,BA72:BD75)-$BW$54
という感じです。
Excelだけで完結している場合はこれでも全く問題無いのです。
学習時はその式に合わせてバイアスが正または負の値になるからです。
ただし、ディープラーニングやニューラルネットワークの書籍やネットの情報を見ると、畳み込みやAffineのバイアス計算は、以下のようになっています。
y = (WX1+WX2+WX3+……) + b
一般的はこちらの式になっているとすると、SONYのNeural Network Consoleも当然この計算式でプログラミングされていると想像できます。
すると、先の2章でも述べたように
y = (WX1+WX2+WX3+……) + (-b)
とすれば同じ意味なのですが、学習後に最適化されると、重みやバイアスの値が全く違ってくるのです。
ということで、前々回8章の畳み込みとAffineの計算式は、全てバイアスを加算する方式に作り変えることにしました。
変更した新たなファイルはGitHubの以下のリンクにアップしておきます。
ファイル名は
cnn(all)4x4_3x3_3node_biasPlus.xlsx
です。
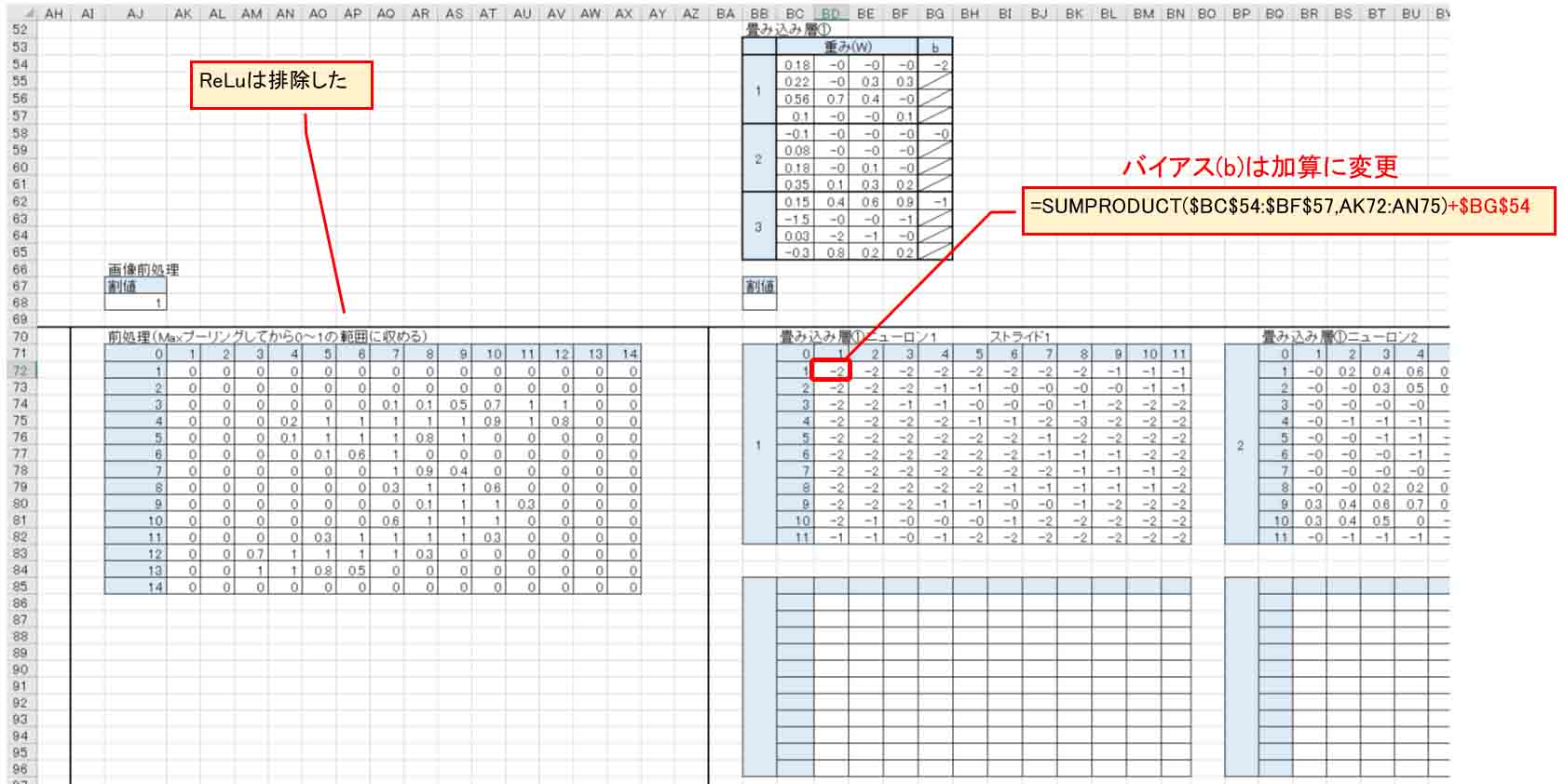
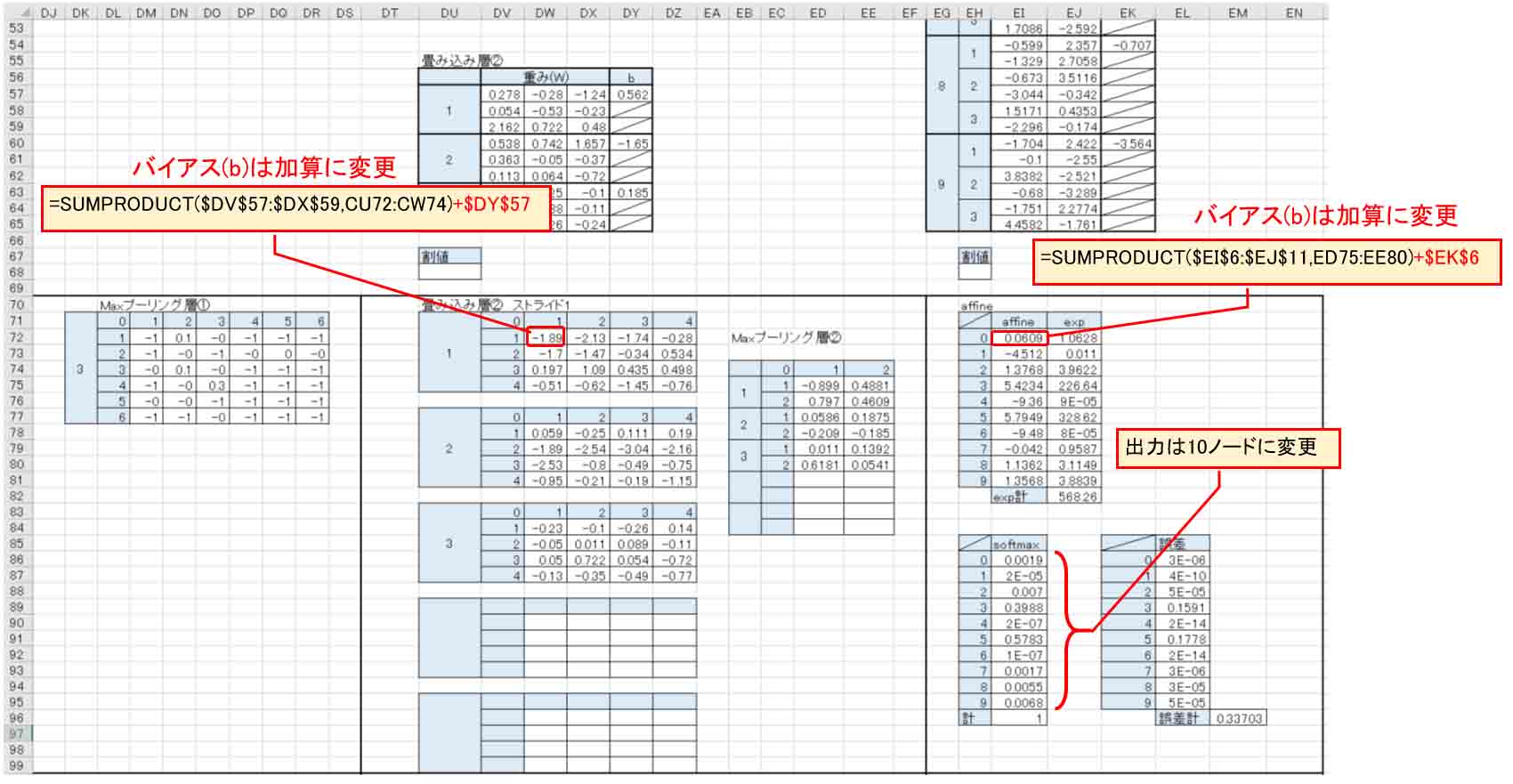
(図04-16)
まず、上図のように画像の前処理ReLuを排除しました。
そして、畳み込み層のバイアスは加算に変更しました。
そして、前回記事4-03節や4-05節で説明したように、MaxPoolingでマス目が割り切れない場合が問題です。
Excelではあまり気にしなかったのですが、SONYのNeural Network ConsoleではPaddingが問題になって来ます。
つまり、入力で負の値が入っていた時に、はみ出た部分をゼロ値としてしまうと、MaxPoolingでゼロを出力してしまうのです。
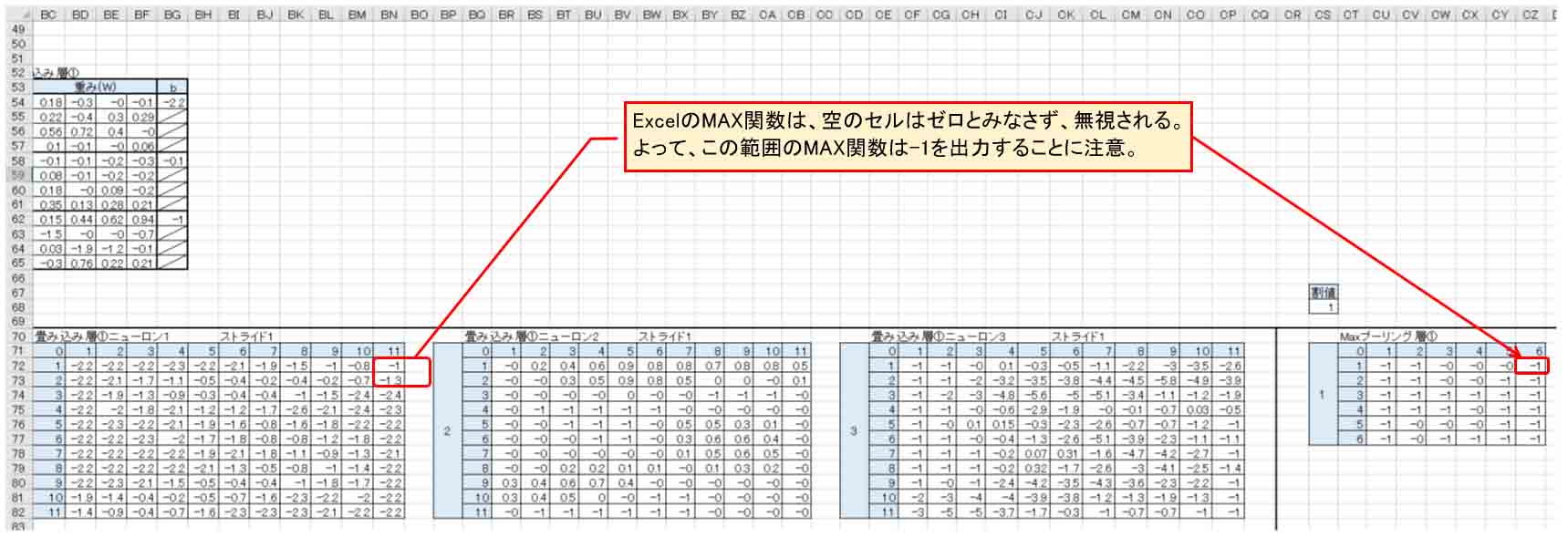
幸い、ExcelのMAX関数は下図の様に空白セルを無視してくれるので、 Neural Network ConsoleのIgnoreBorder : False と同じ計算結果でした。ここは要注意したいところですね。
(図04-17)
2つめの畳み込み層とAffineも下図の様にバイアス(b)を加算に変更します。
そして、出力ノードは10個に変更します。
Affineの重みやバイアスも10ノード分に変更します。
(図04-18)
また、前々回の8章では、ソルバーの制約の為、MNIST学習データは1~9の9種類でしたが、今回、学習はNeural Network Consoleで済ませているので、ソルバーの制約はありません。
よって、MNISTデータセットは0~9の10種類に変更し、キッカリ1000件のデータで評価することにしました。
では、このExcelファイルに先ほど生成した重み(W)とバイアス(b)の値をコピペして評価してみます。
評価と言っても、まずは学習データの正答率を見てみます。
下図のような感じです。
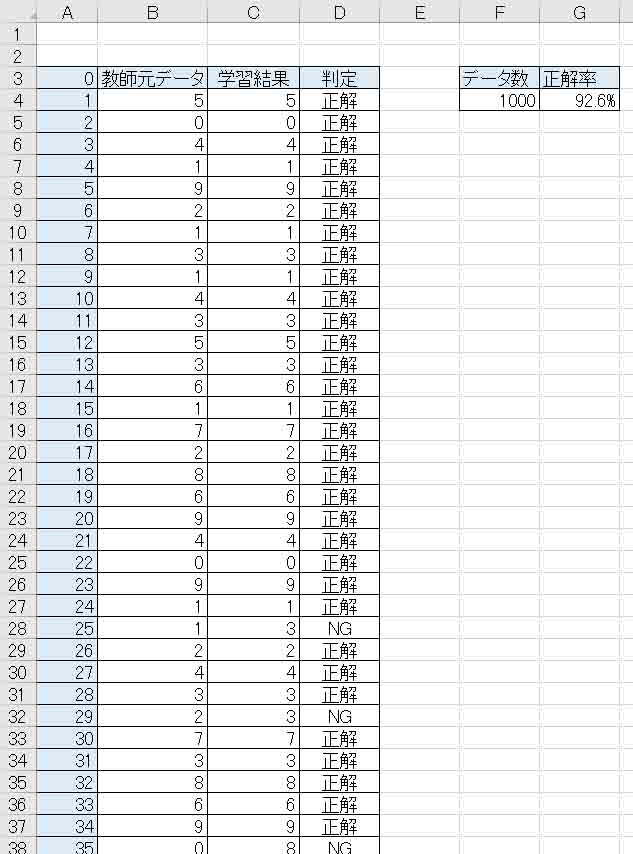
(図04-19)
おっと!
正答率が92.6%出ました。
前々回8章よりも0.1%上がりました。
なかなか良いではないですか!
実は、これは学習用データの正答率なので、Neural Network Consoleとは単純に比較はできません。
ならば、MNISTのテストデータ1000件に変更したらどうなるでしょうか。
テスト用ExcelファイルはGitHubの以下のリンクにアップしておきます。
https://github.com/mgo-tec/test_excel_deeplearning/blob/master/NNC/TEST_cnn(all)4x4_3x3_3node_biasPlus.xlsx
ファイル名はTEST_cnn(all)4x4_3x3_3node_biasPlus.xlsx です。
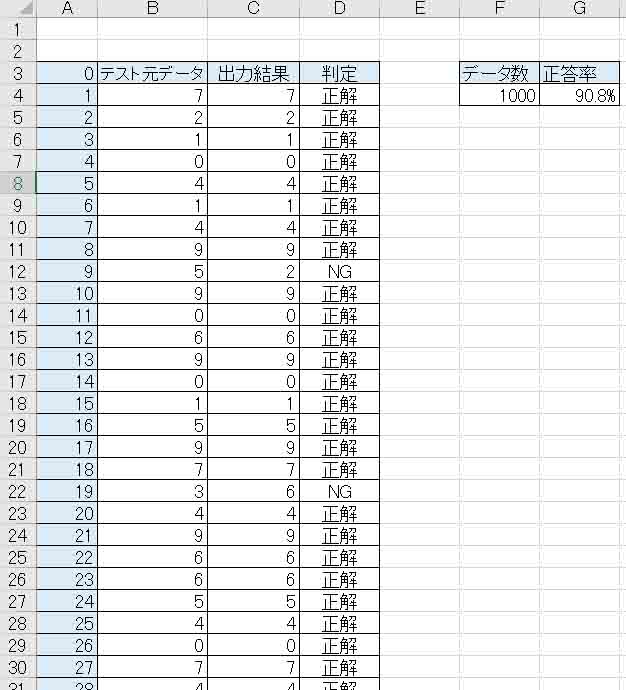
下図のようになりました。
(図04-20)
正答率は90.8%でした。
ま、せいぜい1000件程度のデータですから単純な比較はできませんが、(図03-07)のNeural Network Consoleの正答率とほぼ同じと言えるので、自作のExcel計算式のニューラルネットワークは正しかったといえそうです。
ここまで出来ればESP32やM5Stackやラズパイなどのマイコンに組み込んでプログラミングできそうですね。
いやぁ~、ここまで来るのに長い時間がかかりましたよ。ほんとに。
5.正答率を上げる実験
これまでは前々回記事のExcelで作った畳み込みニューラルネットワークと比較するためもので、正答率がせいぜい91%程度でした。
Excelのソルバーによる制約のために、DepthwiseConvolutionを使ったり、ノード数を3つに制限したりしていました。
正直、これでは実践で使えません。
せめて98%は超えてほしいところです。
ならば、パラメータの制限のないSONYのNeural Network Consoleならばもっと自由に組めて正答率を上げられると思います。
では、いろいろ実験してみます。
5-01. 画像の前処理MaxPoolingを外してみる
4章で作ったニューラルネットワークは、1回目のConvolutionの手前でMNIST画像をMaxPoolingで圧縮していましたが、まずは単純にこのMaxPoolingだけを外してみます。
そして、2つ目の畳み込み層はDepthwise Convolutionではなく、通常のConvolutionにします。
こちらの方が正答率は断然良いです。
すると、こんな感じです。
(図05-01-01)
最後のTanh層を見てみると、出力が5×5マスの3ノードになっていることに注目しておいてください。
そうなると、Affineでは膨大な数のパラメータになっていると思います。
では、重み(W)とバイアス(b)のパラメータ総数を見てみたいと思います。
下図の様に右欄の「CostParameter」をクリックしてみます。
(図05-01-02)
これを見て分かる通り、1つ目のConvolutionで51個、2つ目のConvolutionで84個、Affineで何と760個になってしまいました。
総合計は何と何と895個です!
先の4章で作ったニューラルネットワークが211個ですから、何と4倍以上になってしまいました。
これについては前々回記事の2-4節と本記事の2章を読み返してもらえれば分かるのですが、特にAffineの前の入力パラメータ数が少しでも増えると、その出力がとんでもなく増大することを頭に入れておいた方が良いですね。これは通常のConvolutionも一緒です。
ですから、マイコンに組み込んだり、他のアプリに流用したりする時に、このことを考慮して如何にパラメータ数を減らすかが肝になると思います。
では、これで学習させてみます。
Max Epoch = 1000
としました。
こんな感じです。
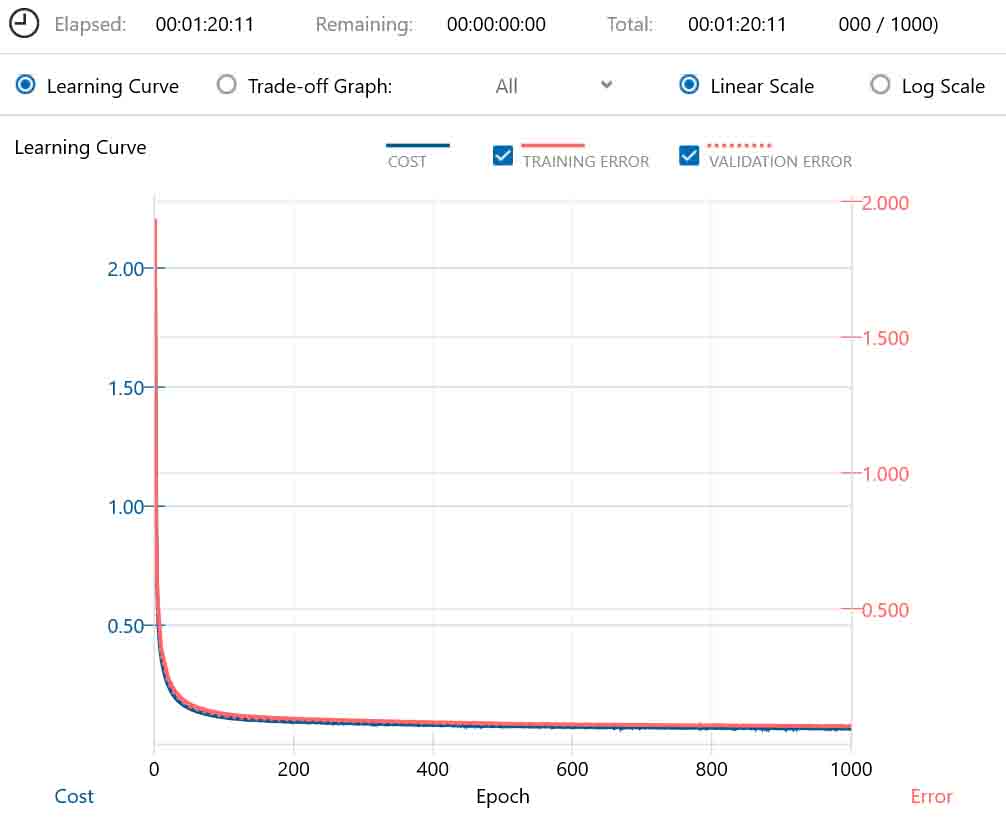
(図05-01-03)
学習時間は1時間20分でした。
では、EVALUATIONの正答率を見てみると、こんな感じです。
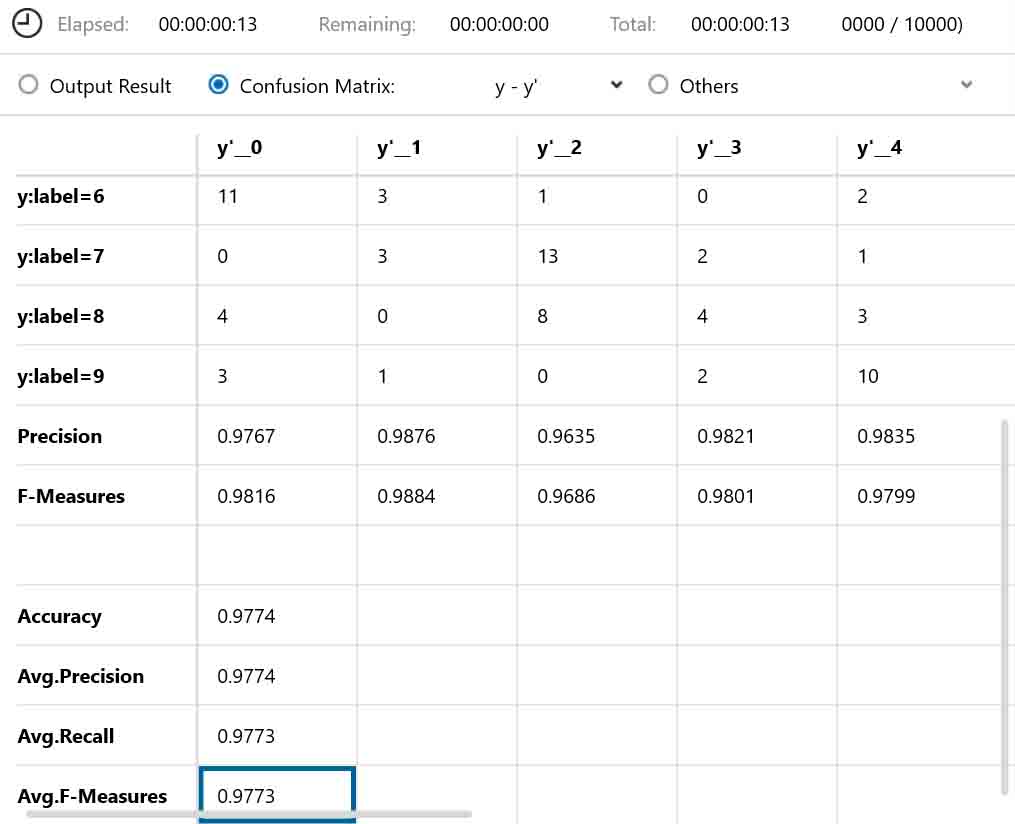
(図05-01-04)
やった!
正答率が97.7%までアップしました。
たかが3ニューロン(ノード)なのに上出来ですね。
これから考えると、やはり前処理で画像を圧縮しない方が正答率は良いですね。
というより、重みフィルターの数が多くなれば多くなるほど正答率が上がるものなのかも知れません。
5-02. ニューロン(ノード)数を増やしてみる
では、今度は画像の前処理MaxPoolingは外さずに、4章のニューラルネットワークの状態のままでニューロン(ノード)を3から5つに増やしてみます。
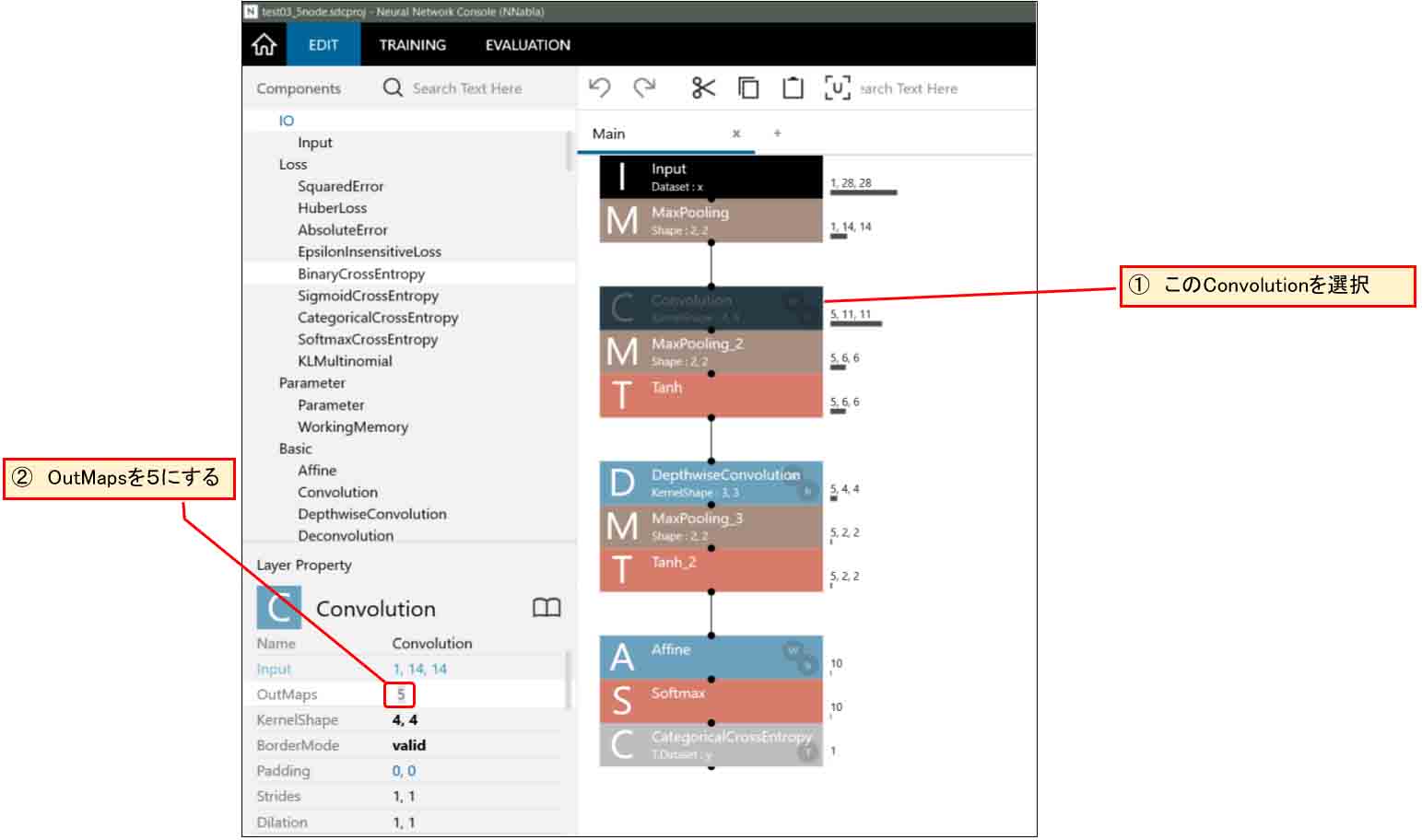
下図の様に一つ目のConvolutionの「OutMaps」を5に変更します。
(図05-02-01)
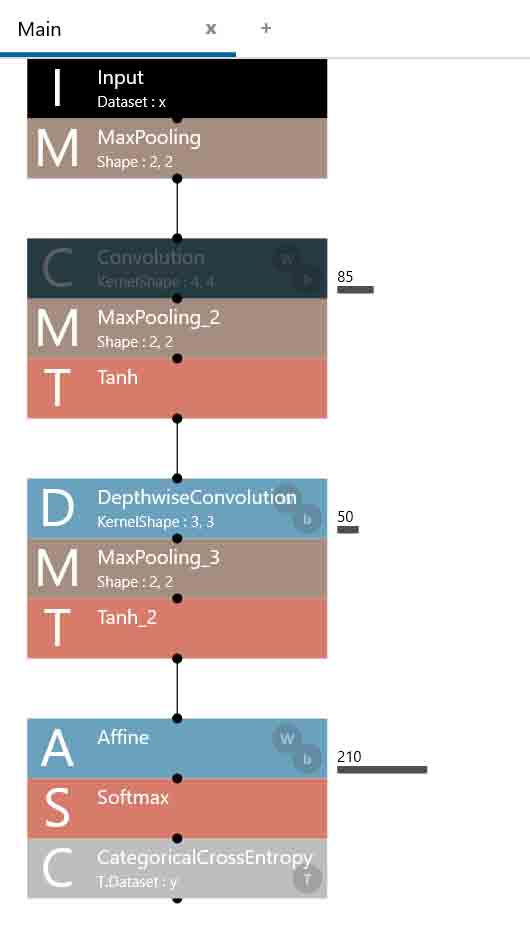
そして、CostParameterを見てみると、以下のようになりました。
(図05-02-02)
重み(W)とバイアス(b)の総合計は、
85 + 50 + 210 = 345
となり、5-01節の895個よりはかなり節約できています。
では、これを学習させて、EVALUATION(評価)させてみるとこうなりました。
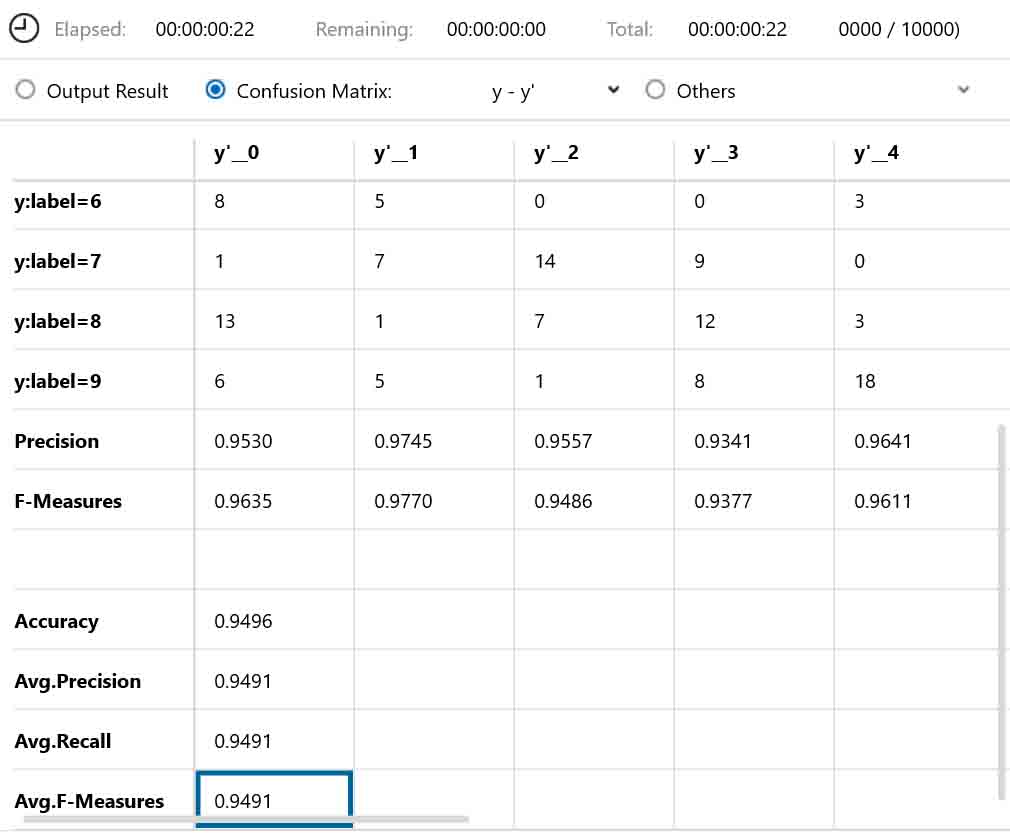
(図05-02-03)
学習時間は私の環境で1時間13分でした。
正答率は94.9%でした。
このことから、単純にConvolutionの出力ニューロン(ノード)数を増やせば正答率を上げられるということが分かりますね。
5-03. 最初のConvolutionで5ノード、次のConvolutionで3ノードにしてみる
では、別の方法として、5-01節のニューラルネットワークで、最初のConvolution(畳み込み層)でOutMapsを5にして、出力を5ノードにして、次のConvolution(畳み込み層)でOutMapsを3にして、出力を3ノードに減らすということをやってみます。
こうする理由は、5-01節の正答率が高かったのと、5-02節でニューロンの数を多くした方が正答率は高くなるということからです。
これは、今回は割愛しますが、Excelで作ると面白いと思いますよ。
最初は計算式に迷うと思いますが、2章で述べたことを頭に入れればできると思います。
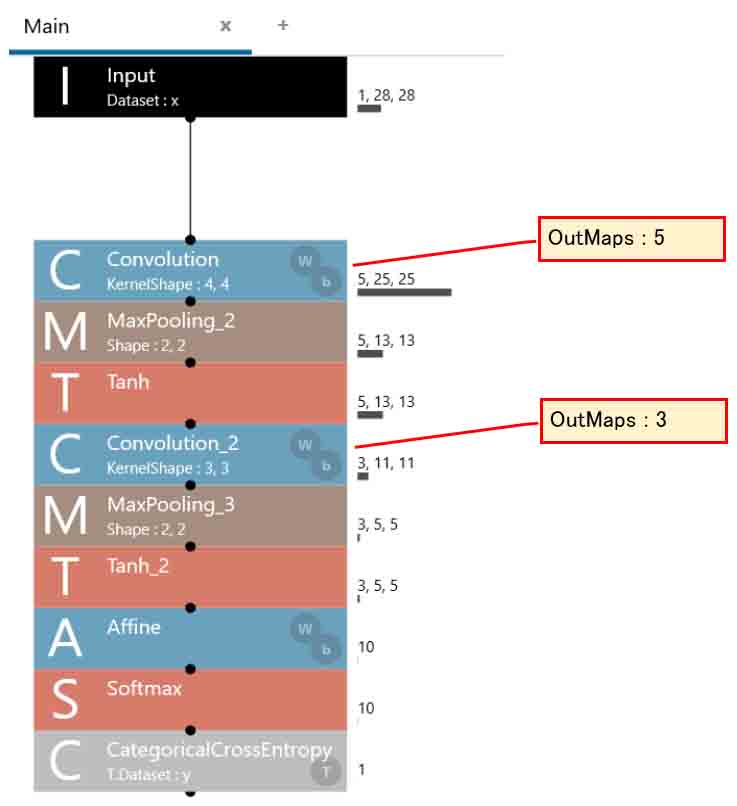
では、Neural Network Consoleではこんな感じになります。
(図05-03-01)
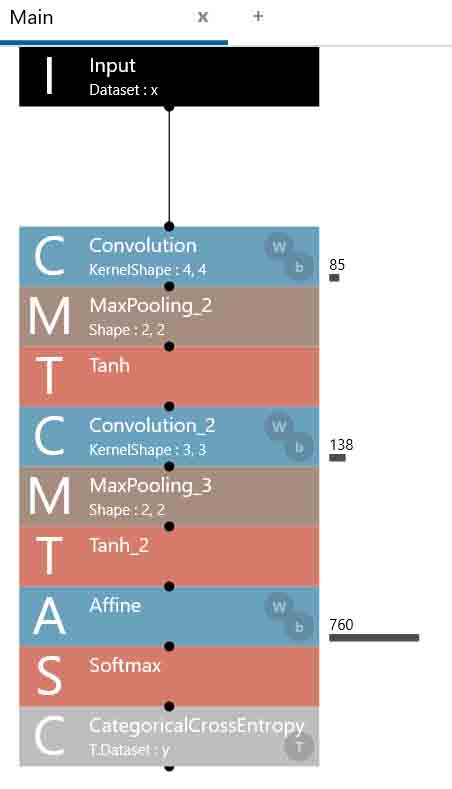
では、CostParameterを見てみるとこんな感じです。
(図05-03-02)
85 + 138 + 760 = 983
となりました。
なんと、5-01節のCostParameter総数よりも多くなってしまいました。
注目して欲しいのが、2つ目のConvolutionでパラメータ数が大幅に増えているという事です。
これは先の2章がわかっていれば理解できると思います。
では、これを学習させて、EVALUATIONで評価させるとこんな感じになりました。
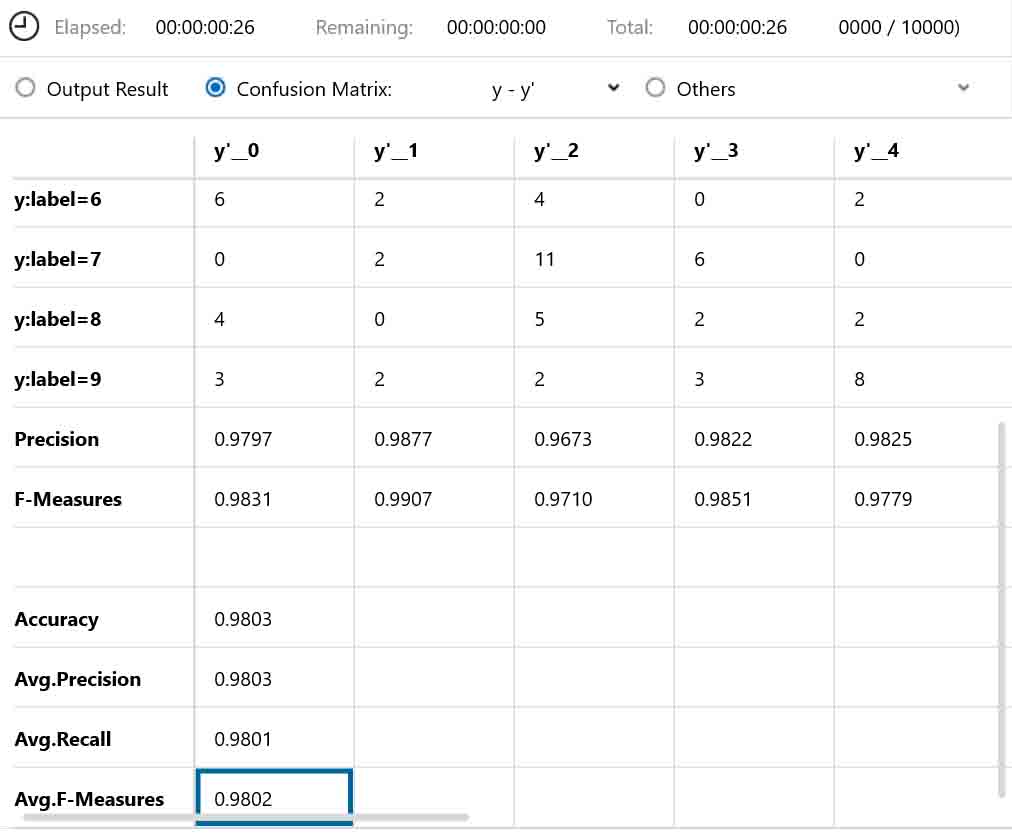
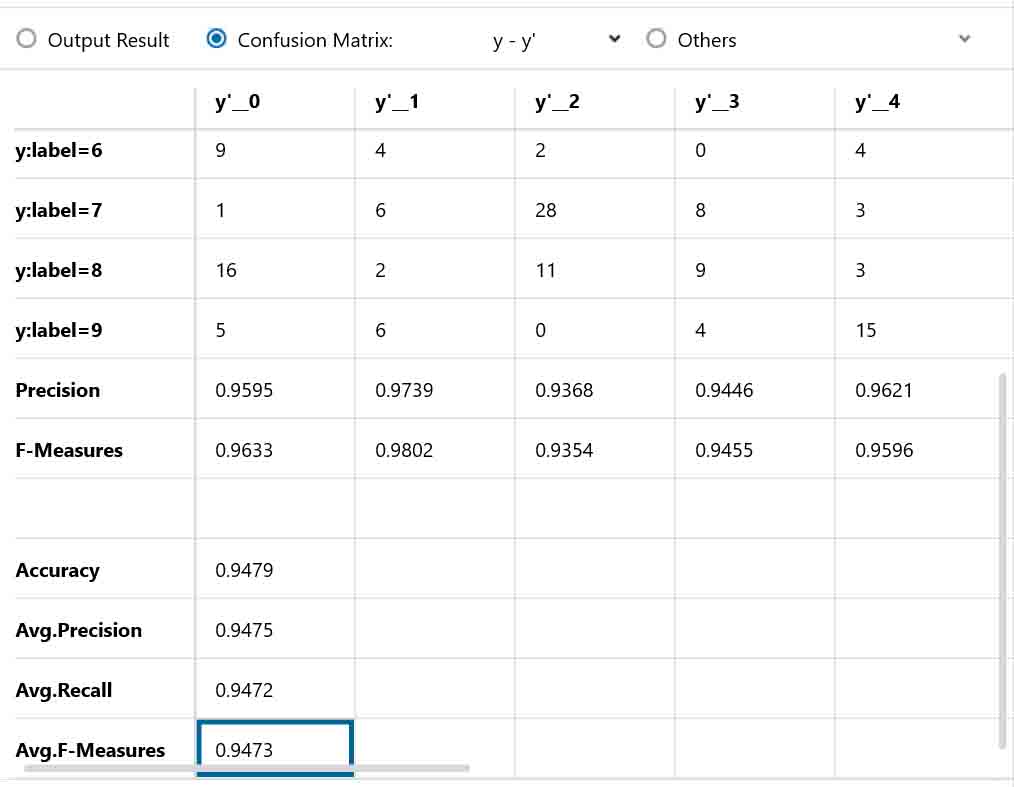
(図05-03-03)
やったね!
正答率が98%を超えて、目標値に達しました。
ここまでくれば実用に十分だと思います。
本当は2つ目のConvolutionのOutMapsも5にすれば、もっと正答率が上がります。
実際に両方ともOutMapsを5にして学習させてみましたが、正答率は98.3%まで上がりました。
ただし、CostParameterは、
85 + 230 + 1260 = 1575
となり、5-01節のほぼ倍にまで膨れ上がりました。
これでは非力なマイコンに組み込むのは厳しいと思います。
5-04. 最初のConvolutionの重みフィルターを6×6マスにしてみる
前節で正答率は98%まで上げられましたが、CostParameterの数が多すぎてマイコンに搭載するには厳しいので、コストを削減しつつ正答率を上げる工夫をしてみます。前節のニューラルネットワークを少し改変して、最初のConvolutionで重みフィルターを6×6マスにしてみます。
以下の感じです。
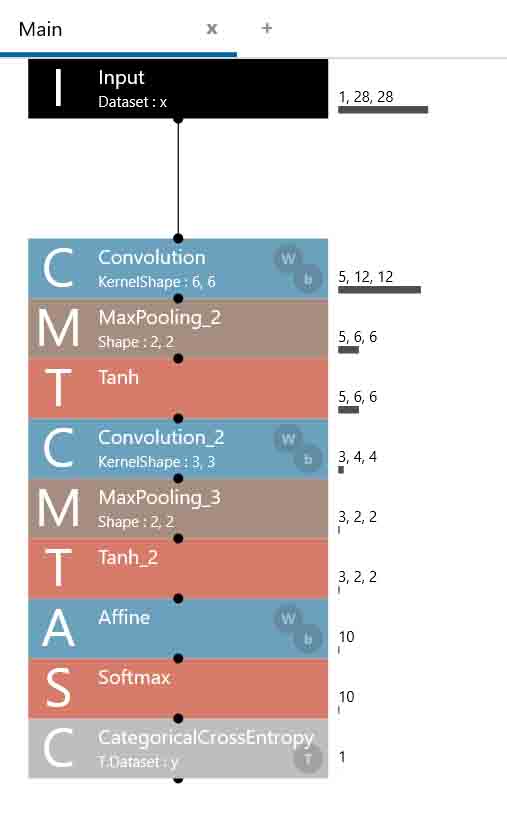
(図05-04-01)
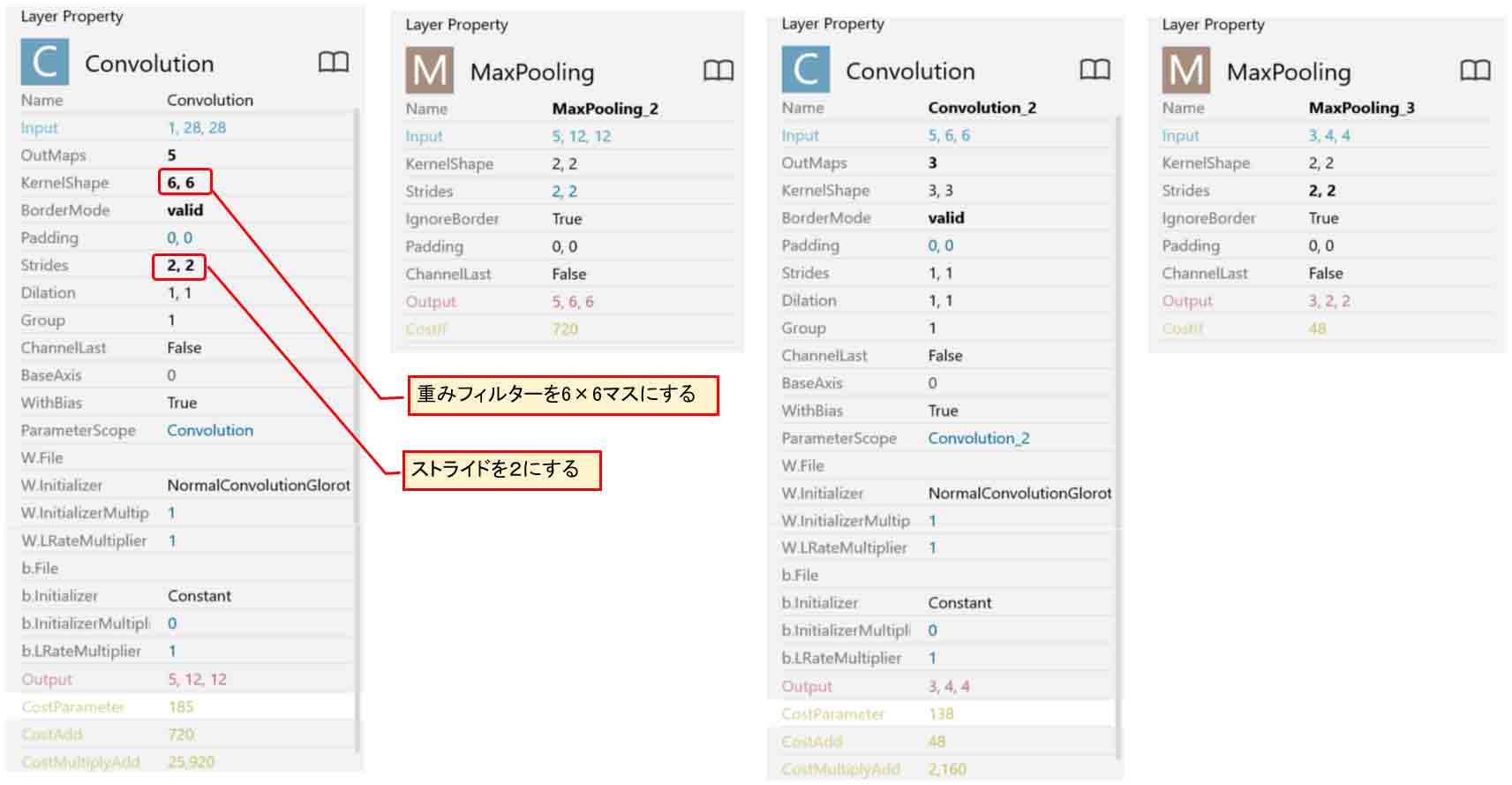
そして、各パラメータは以下の感じです。
最初のConvolutionの重みフィルターはKernelShapeを6,6とし、ストライドを2,2にします。
MaxPoolingは2×2マスでストライドは2です。
2つ目のConvolutionは入力が5ノードで、OutMapsを3として、3ノード出力とします。ストライドは1にします。
(図05-04-02)
なぜ、こうするかというと、前々回の記事3章でふと思ったのが、重みフィルターのマスを大きくした方が、28×28 pixelのMNIST画像は認識率が高くなりそうだと想像したからです。
実際に何度もNeural Network Consoleで実験してみて、4×4マスのフィルターよりも大き目の方が正答率が高かったからです。
それにプラスして、ストライドを2にすると、その後のコストを抑えることができました。
そして、2つ目のConvolutionではストライドを1に抑えた方が正答率が高かったのでそうしました。
また、MaxPoolingは、ストライドを大きくしたり、KernelShapeを大きくして重ね合わせたりすると結果は良くなかったので、デフォルト設定の2×2カーネルでストライド2としました。
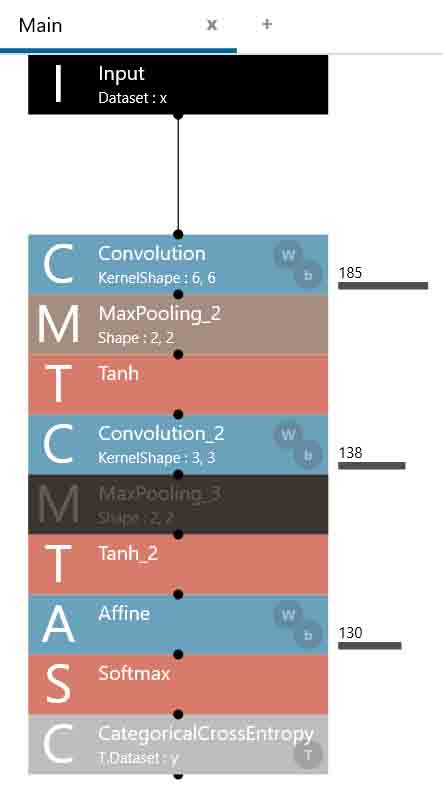
では、CostParameterの値を見てみると以下の感じでした。
(図05-04-03)
185 + 138 + 130 = 453
となりました。
前節の983に比べれば、半分以下に抑えられました。
これでも最初のConvolutionのコストは大きいですね。
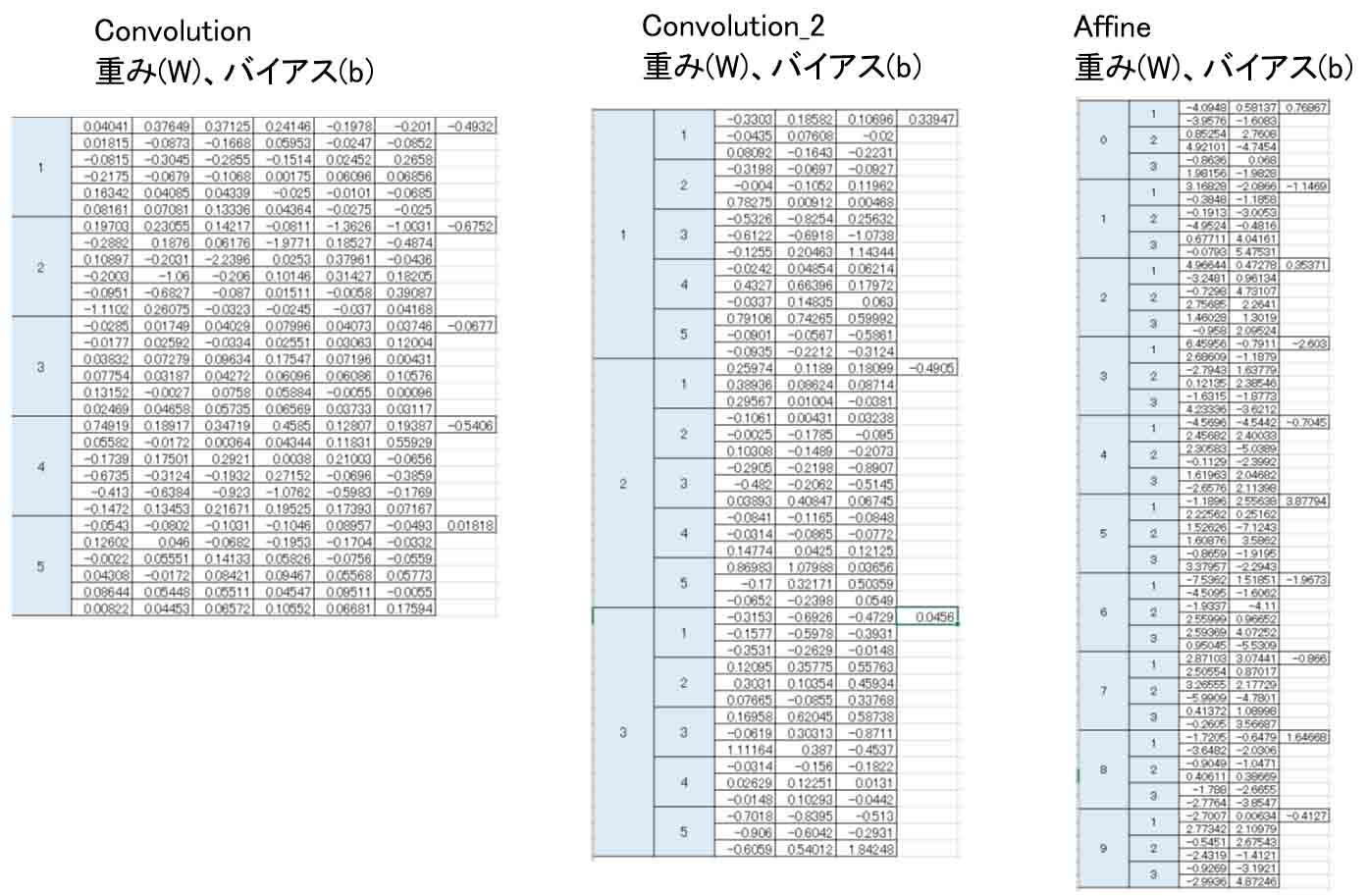
実際にExcel表にしてみると、こんな感じです。
(図05-04-04)
こうやってExcelに落とし込んでみると、膨大なパラメータ数ですね。
コストという意味合いが良くわかります。
では、これをMaxEpoch = 2000 で学習および評価させてみます。
結果は、こんな感じになりました。
(図05-04-05)
学習時間は2時間20分かかりました。
正答率は94.7%となり、前節の98%には到底及びませんでした。
5-02節とほぼ同じ結果でした。
やはり、最初のConvolutionでストライドを2にしてしまったことが響いているようです。
コストを500以下に抑えた場合は、94%前後の正答率で頭打ちになってしまうかもしれないですね。
もっと良い方法があったら教えてください。
以上より、この章の実験で分かったことこんな感じです。
●画像の前処理は極力避けた方が正答率は良い。
●最初のConvolutionのOutMapsを増やす、つまり出力ノードを増やした方が正答率は良い。
●DepthwiseConvolutionよりもConvolutionを使った方が正答率は良い。
●ノード数が多いと、2回目のConvolutionではコストが膨大になることに要注意。
●重みフィルターが多いニューラルネットワークほど正答率は良い。
●コストを500以下に抑えた場合、正答率は94%くらいが限界だった。
結果的に重みフィルターの数、つまりコストパラメータの数にネットワークが制限され、それによって正答率も変わるということです。
非力なマイコンにニューラルネットワークを搭載するには、最後のAffineで膨大な数のコストが発生するので、その手前でいかにコストを抑えるかが重要になってきます。
2回目のConvolutionでノード数を減らして、コストをコントロールするということだと思います。
こんな感じで、SONYのNeural Network Consoleは気軽にネットワーク構造を変えて学習を試すことが出来るので、ホントに優れたツールだと思いますね。
6.まとめ
以上のように、SONYのNeural Network Console は、学習後の重み(W)やバイアス(b)をエクスポートできることが分かり、ESP32やM5Stackおよびラズパイなどのマイコンやアプリに流用できることが分かりました。
そして、ConvolutionとDepthwise Convolutionの違いも分かって、正答率を上げるには画像の前処理を外したり、ノード数を増やしたりすれば良いことも分かりました。
ただ、注意しなければならないのは、2回目のConvolutionが要注意で、何も知らないで使うと重みフィルターのコストが膨大になってしまうということです。
そのコスト数をよく考えてコントロールしてニューラルネットワークを組む必要があることが分かりました。
また、Neural Network Consoleだけでは、パラメータの計算方法とか、コストの数などがブラックボックスになっていて分かり難いので、Excelと併用して実験してみるとコストの意味合いが良くわかって理解が深まるのでお勧めですよ。
では、これでマイコンにニューラルネットワークを搭載する準備が整ったので、次回はいよいよESP32やM5Stackに応用してみようと思います。
今回はここまでです。
ではまた。。。
Amazon.co.jp 当ブログのおすすめ
















コメント