ゼロからディープラーニングを勉強してみる ～Excel編その２。ニューラルネットワークと学習～

こんばんは。

前回記事に引き続き、ゼロからディープラーニングを勉強してみるExcel編の第２弾です。
いよいよニューラルネットワークを組んでみて、ニューロンの数の意味や隠れ層の役割、教師データで学習させて重みやバイアス値の最適解を得るというディープラーニングの一部を体感してみたいと思います。

前回記事では、バイアス値（閾値）やシグモイド関数について利点を実感しましたが、自己流計算式ではすぐに限界に達しました。
特に、○印と×印で同じ画素が重なる場合、IF文条件分岐を多量に作らねばならず、更に画素が増えるととても無理でした。
ならばニューラルネットワークを組んでディープラーニングにすると、それを解決できるのかを見ていきたいと思います。

今まで書籍を斜め読みしたり、ネットの情報をサラッと読んだだけではイマイチ理解できていなかったことが、今回の実験で実際に自分の手でニューラルネットワークを組んでみると、その特徴が良く解るようになってきました。
もはや、自分の中でAIやディープラーニングについては、単なる数値計算だけっていう概念に変わりつつあります。

だけど、普通、プログラミングを組む場合、閾値は自分で予想して入力して、そして実験して閾値を修正するという流れですよね。

今までのプログラミングと大きく違うところは、教師データを与えることによって重みや閾値が自動的に割り出されるというところです。
ディープラーニングは正にそこが違うんです。
そして、学習後は複雑なIF文等の条件分岐を組まなくても、重みと閾値だけの数値データ群と単純な計算だけで結果が導き出されるんです。
何とも不思議な感じがしました。

ということで、これから書籍を参考にしながら勉強していき、疑問点をダラダラと書きます。
以下、前回記事と同じように、3×3 pixel の超簡単な画像で、○印か×印かを判定する場合を例に考えます。

なお、この分野はド素人なので、誤りや勘違いが多々あると思います。
気が付いたことがありましたらコメント投稿等でご連絡いただけると幸いです。

【目次】

参考書籍
自己流サンプルファイル

1. 入力と出力だけのニューラルネットワークを組んでみる（隠れ層無し）
2. ディープラーニングの肝は誤差が最小になるような最適な重みとバイアスを設定すること
3. ソルバーを使って誤差の最小値を得て、重みとバイアス（閾値）の最適値を得る
   • ソルバーをインストールする
   • ソルバーで重みとバイアス値の最適解を自動計算させてみる
4. 教師データを追加すると、あら不思議
5. ニューラルネットワークの隠れ層を入れてみる
6. ニューラルネットワークの隠れ層のニューロンを増やしてみる
7. 重みとバイアスのスタート位置を変え、更に小さい極小解を導いてみる
8. 重みとバイアスに負の値を許容させたら、全問正解になった
9. 隠れ層を追加したら結果が良くなるのか？
10. まとめ

参考書籍

前回記事と同様、以下の書籍を参考に進めていきます。
まずはこれだけ読めばよいでしょう。KINDLE版と書籍版があります。

【題名】
Excelでわかるディープラーニング超入門

【著者】
涌井 良幸、涌井 貞美

【KINDLE版】

【書籍版】

もっと深く知りたければ以下の書籍です。
ただ、これは難解です。

【題名】
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装

【著者】
斎藤　康毅

自己流サンプルファイル

今回の勉強で作ったサンプルファイルをGitHubの以下のページに置いておきます。

https://github.com/mgo-tec/test_excel_deeplearning

今回使うファイルは
neural_network01.xlsx
というファイルです。
Excelのシート名はここで紹介した図の番号です。

１．入力と出力だけのニューラルネットワークを組んでみる（隠れ層無し）

では、まず、先ほど紹介した参考書籍
「Excelでわかるディープラーニング超入門」
に習いながら、独自にいきなりニューラルネットワークを組んでみます。

ただ、この本通りにExcel表を組むと、ニューラルネットワークの位置関係が分かりにくかったので、自己流にExcel表を組んでみました。

書籍を予め読んで、いまいちニューラルネットワークやディープラーニングが理解できなくても全然良いのです。
とにかく実際に組んで動かしてみれば、いずれ分かって来ます。

まずは、先ほどの書籍を読んで、ニューラルネットワークを組みますが、なぜ隠れ層というものが無ければいけないのかというところに疑問がわきました。

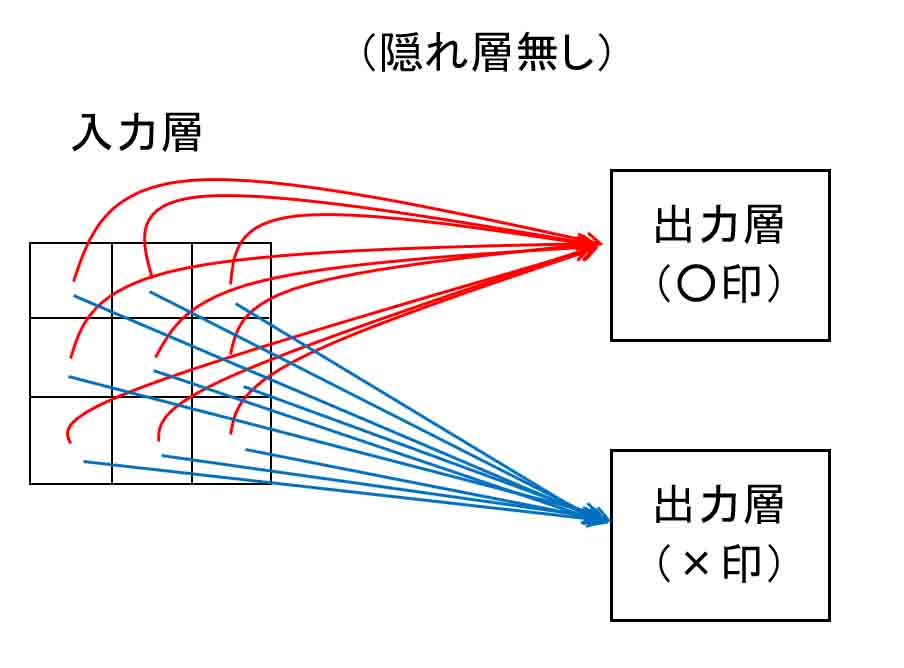
そこで、まず、入力層→出力層という隠れ層の無い超単純なニューラルネットワークを組んでみます。
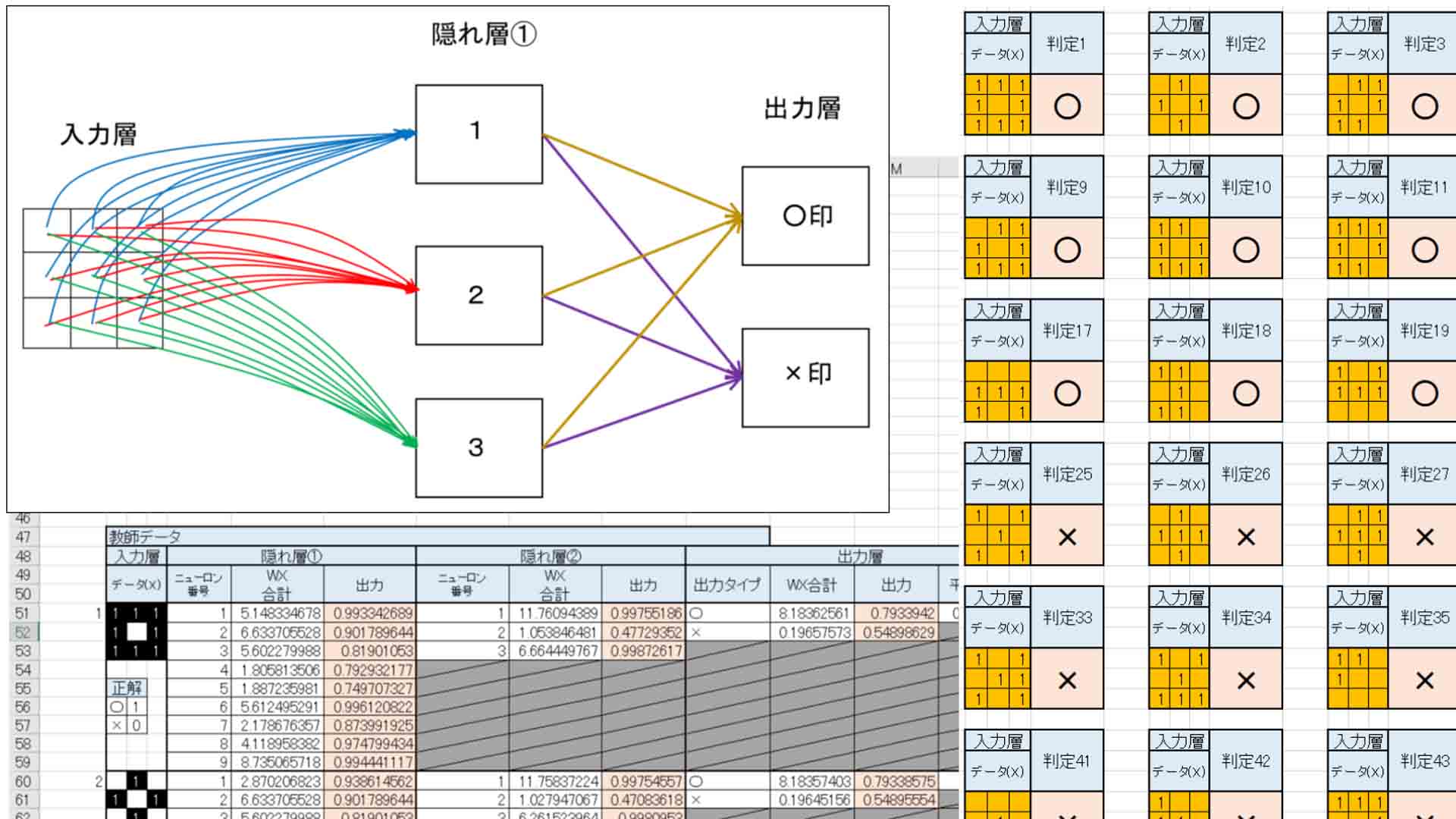
概要はこんな感じです。

（図1_01）

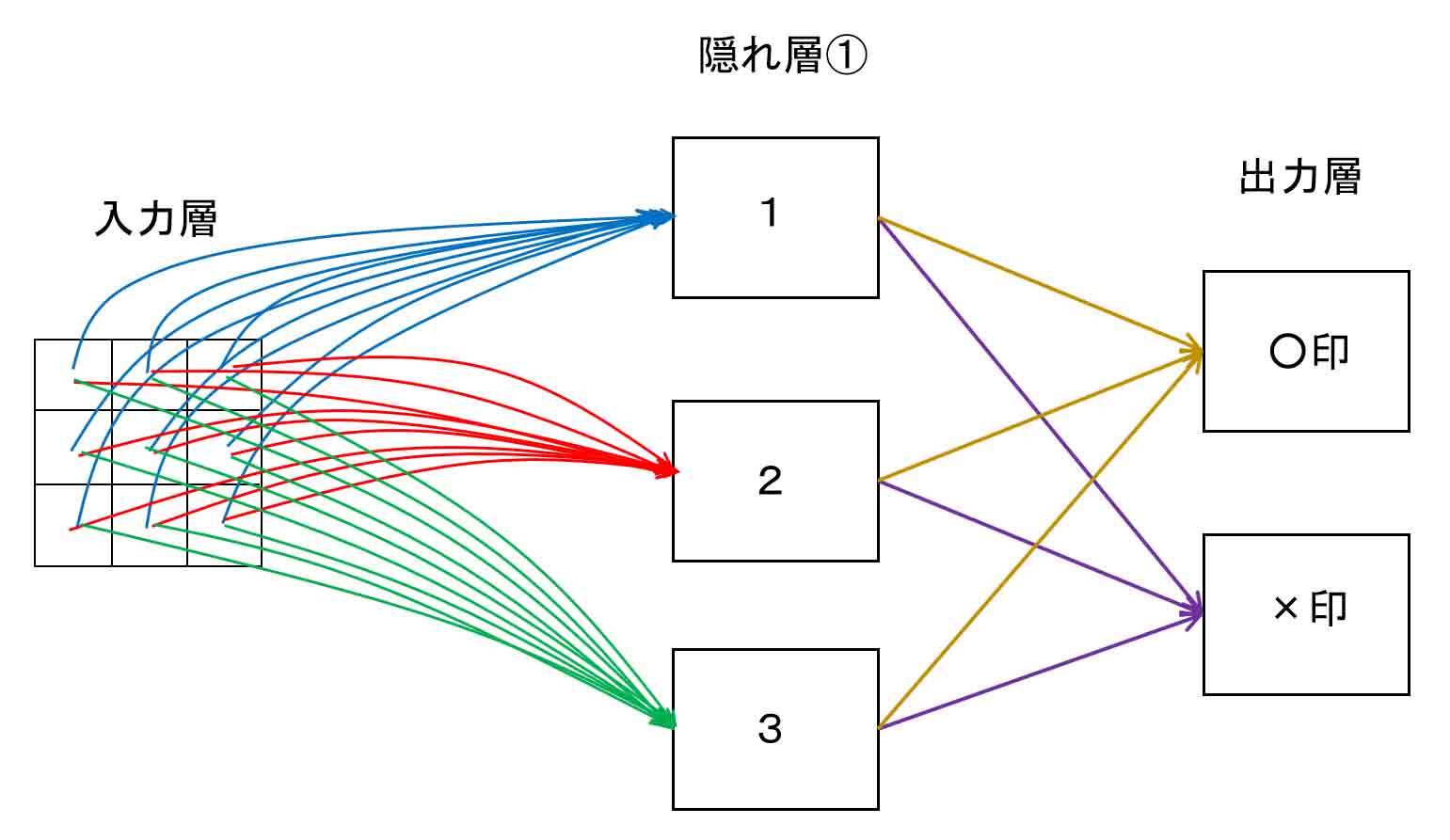
○と×だけの判定なので、出力層は２つです。

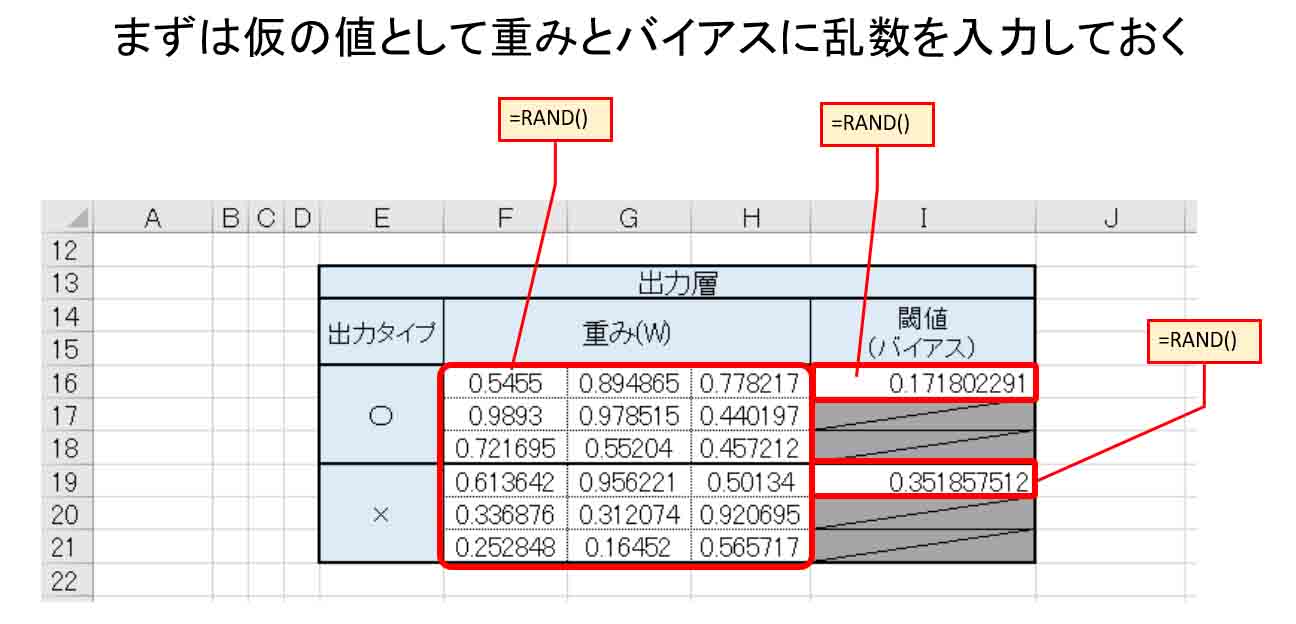
次に、Excel で出力層の重みとバイアス（閾値）を設定しておきます。
と言っても、どう重みを付ければ良いのか全く未知なので、ここではあくまでも仮の値として乱数を入力して置きます。
乱数は、セルに

=RAND()

と入力しておけば、0～1の間の乱数を自動で出力してくれます。
下図の様な感じです。

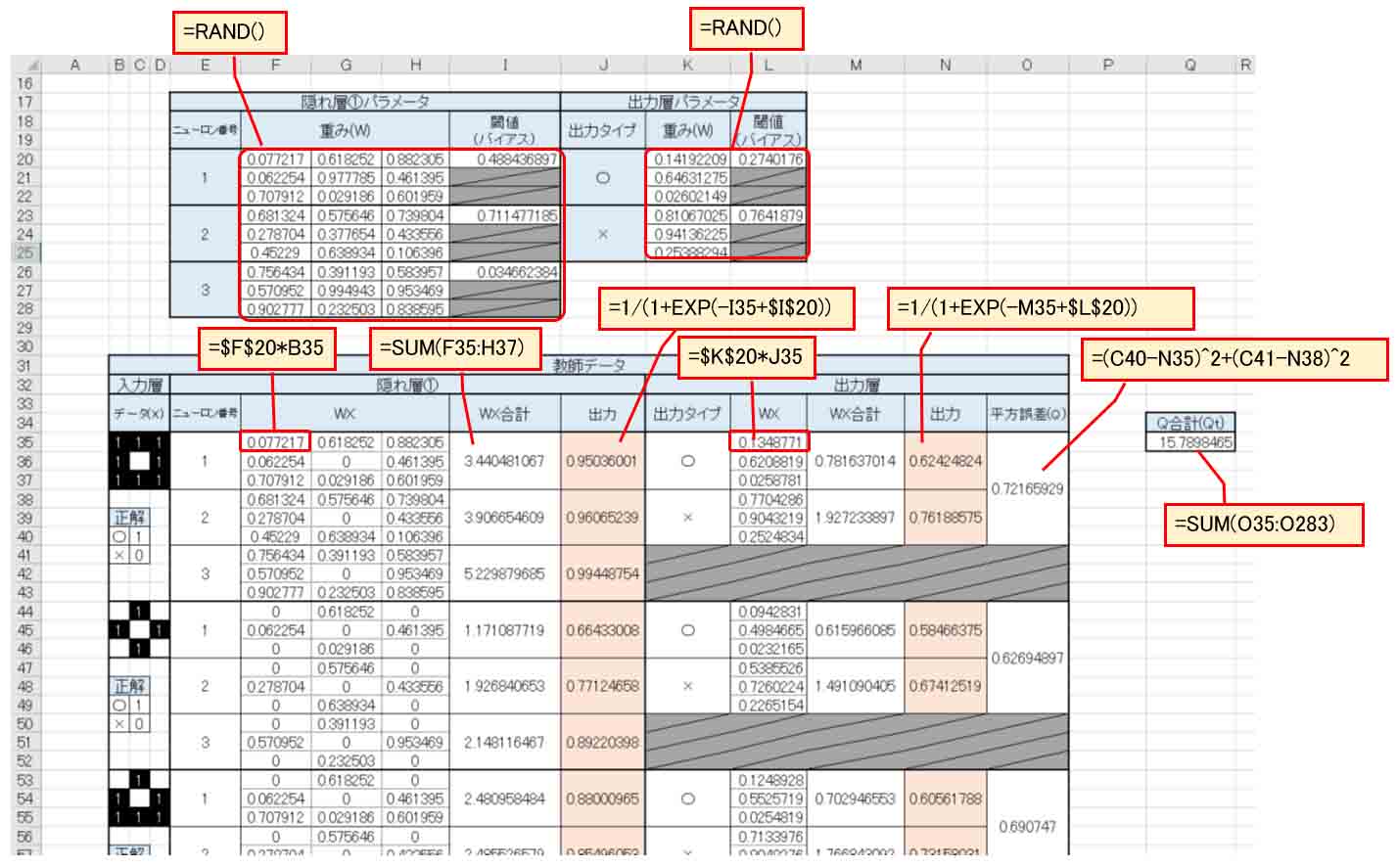
（図1_02）

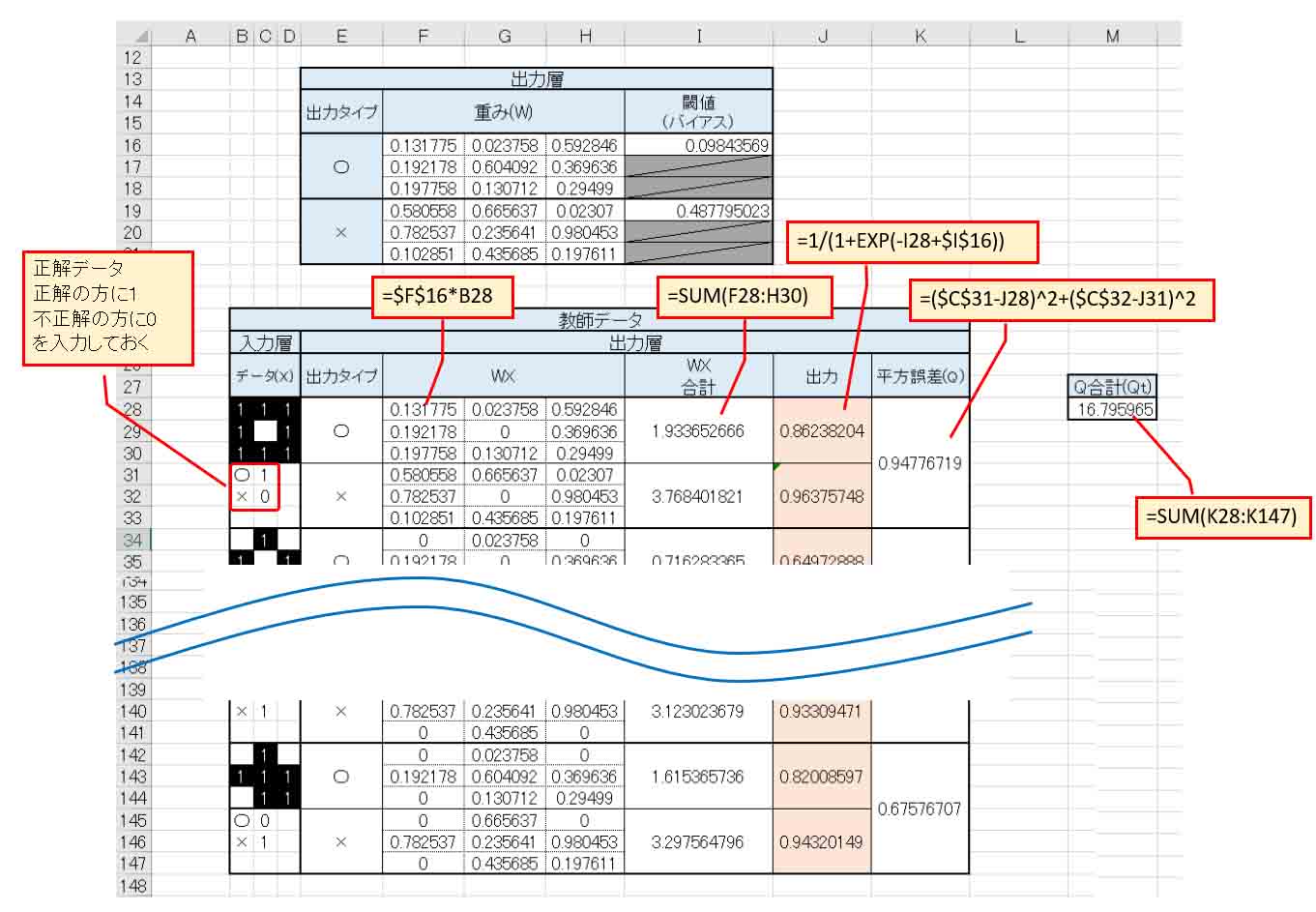
次に、教師データを入力します。
先ほど紹介した書籍、「Excelでわかるディープラーニング超入門」に習って、下図の様に入力しておきます。
教師データは前回記事の（図3_01）のデータと同じです。

（図1_03）

入力層には、○印として与えられたデータを入力し、その下に正解データとして、○印ならばそこに1を入力して置き、×印は0にしておきます。
出力層は２つあるので、○印としての出力、×印としての出力それぞれに、先ほど乱数で入力した重み(W)と入力データ(X)を掛け合わせ、W*Xの合計値を算出し、バイアス（閾値）を入れ込んだシグモイド関数で出力させます。
シグモイド関数については前回記事を参照してください。

そして、前回と異なるのは、平方誤差があることです。
平方誤差とは、書籍「Excelでわかるディープラーニング超入門」を読んでいただければ分かると思うのですが、要するに、正解データと出力データの誤差です。
ただ、2乗しているところがミソです。
なぜ、2乗しているのかと言えば、ただ単にマイナス（負の値）にならないように2乗しているだけと思えば分かり易いのではないかと思います。
その平方誤差が小さければ小さいほど良いというわけです。
つまり、平方誤差の合計値が最小であれば、重み(W)とバイアス（閾値）が最適だというわけです。
ただ、（図1_03）を見ると、重みが乱数なので、誤差が大きくて使えないデータですね。

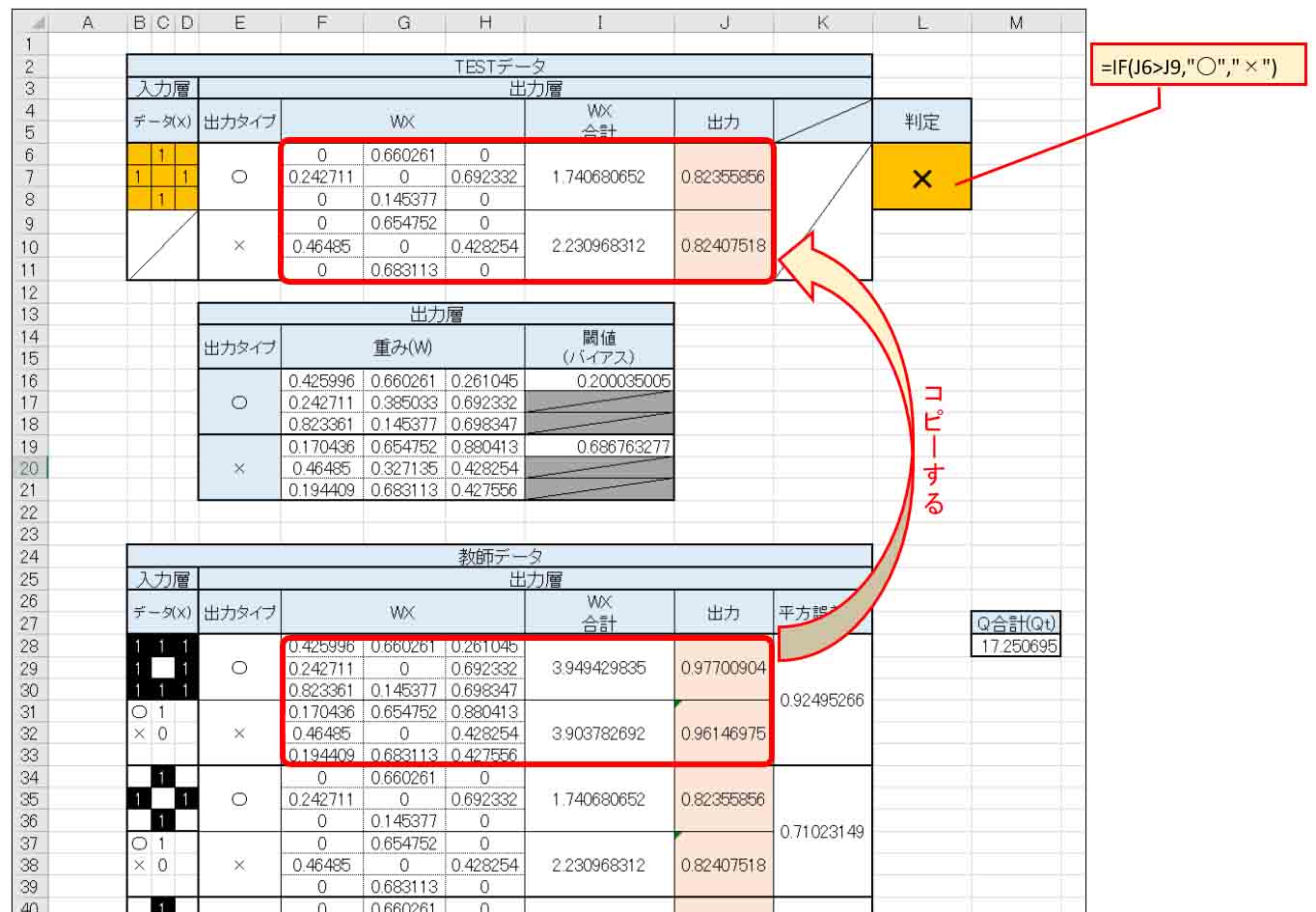
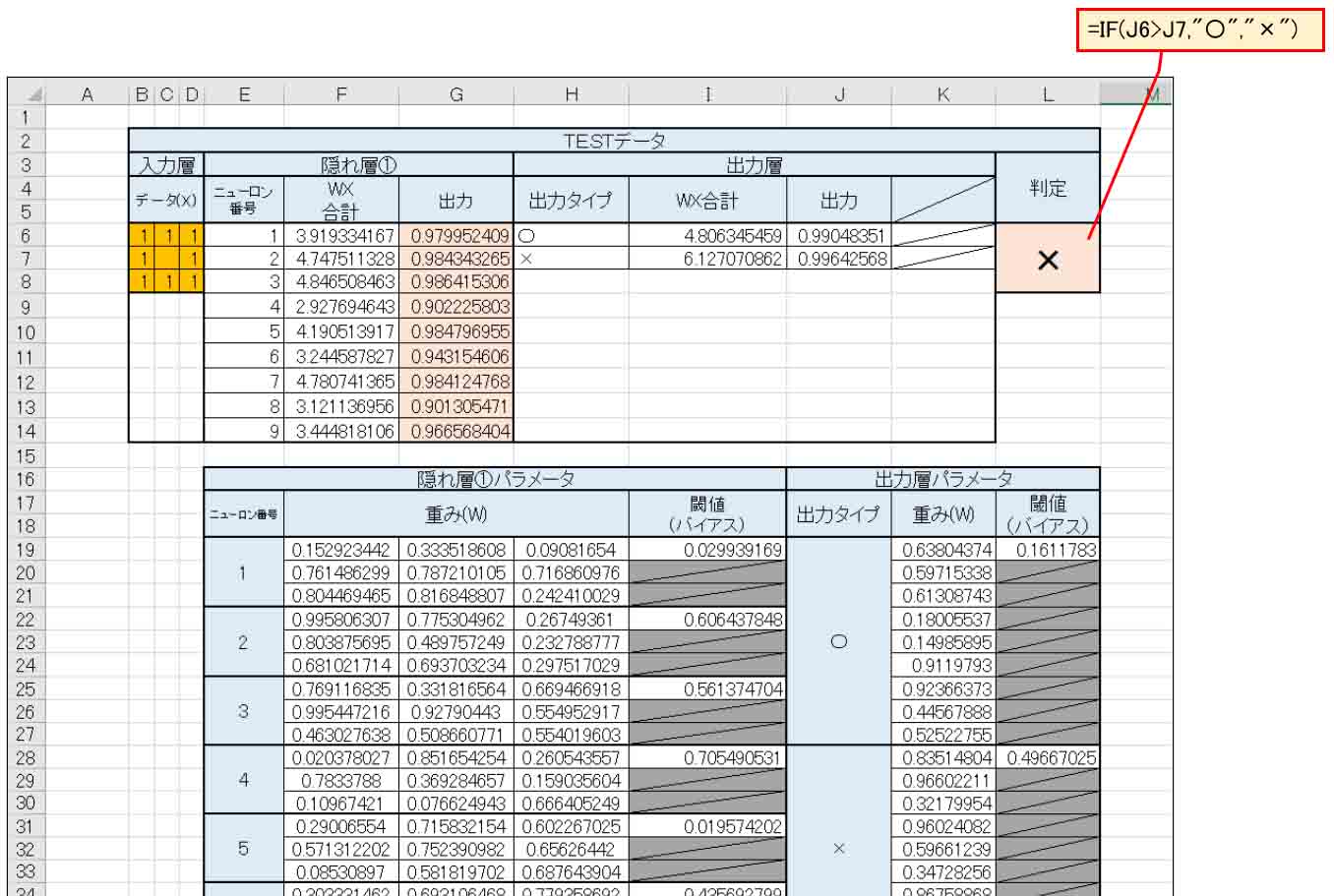
次に、TESTデータ入力欄を作成します。
下図の様に教師データの部分をコピーします。
そして、「判定」については、○印の出力値が大きければ○と判定。それ以外は×と判定するようにしました。

（図1_04）

２．ディープラーニングの肝は誤差が最小になるような最適な重みとバイアスを設定すること

では、隠れ層が無い入力と出力だけのニューラルネットワークでどこまでできるか実験してみます。

先ほど述べたように、各々の教師データの平方誤差が0に近ければ良いということは、平方誤差の合計値(Qt)がゼロに近い最小値であれば良いことは分かりますね。

そうなるように重み(W)とバイアス（閾値）の値を調整してあげれば良いということがExcel表から分かりました。

では、そうなるような出力層の重み（Ｗ）とバイアス（b）はどういう値にしたら良いのでしょうか。

なんと、Excelにはとっても便利なツールがありました。
それはソルバーというものです。

ソルバーを使うと、重み（Ｗ）とバイアス（ｂ）の値を自動的に少しずつ変化させて、平方誤差の合計値(Qt)が最小になるような値を計算してくれて、重み（Ｗ）とバイアス（ｂ）の値を乱数から差し替えてくれます。
メチャメチャ便利ですね。
これは先ほど紹介した参考書籍「Excelでわかるディープラーニング超入門」を読んで初めて知りました。

ディープラーニングの肝はこの誤差の最小値を計算するところにあるのだと思いました。
それをプログラミングできれば、マイコンでもディープラーニングができそうな気がしてきました。

では、次ではそのソルバーについて説明していきますが、一つ注意点があります。
ソルバーはあくまで極小の時の値なので、全体の最小値ではないということを常に留意しておくことが必要です。
ここは要注意ですね。
それについては、参考書籍「Excelでわかるディープラーニング超入門」に書いてありますし、第７章でも実験しているので、おいおい分かって来ると思います。

３．ソルバーを使って誤差の最小値を得て、重みとバイアス（閾値）の最適値を得る

では、先に述べたように便利なソルバーを実際に使ってみます。
ソルバーは、Excelのアドインで、追加料金なしで使えるツールです。
ソルバーを使うと、簡単に最適解（実際は極小解）を自動で割り出してくれて、重みやバイアス値を書き換えてくれます。
これはExcelでディープラーニングをする為の肝となるアプリです。
これが無いと、Excelでディープラーニングができません。
本当は自力で数式を組んで最適解を求めたいのですが、今回はニューラルネットワークの動きを体感したい為、まずはソルバーに頼り切ってみます。

ソルバーをインストールする

参考書籍「Excelでわかるディープラーニング超入門」にも書いてありますが、ここでもソルバーのインストール方法を説明しておきます。

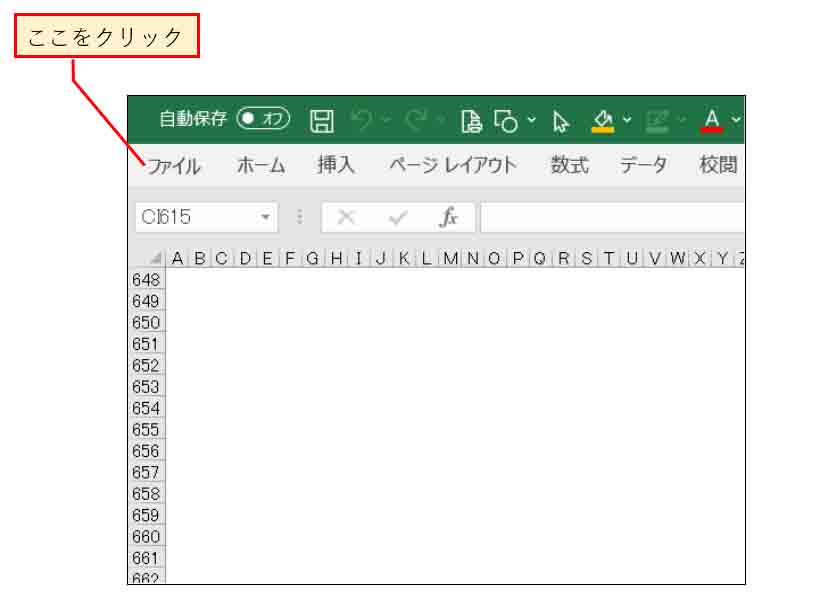
まず、下図の様にExcel画面の「ファイル」をクリック。

（図3_01）

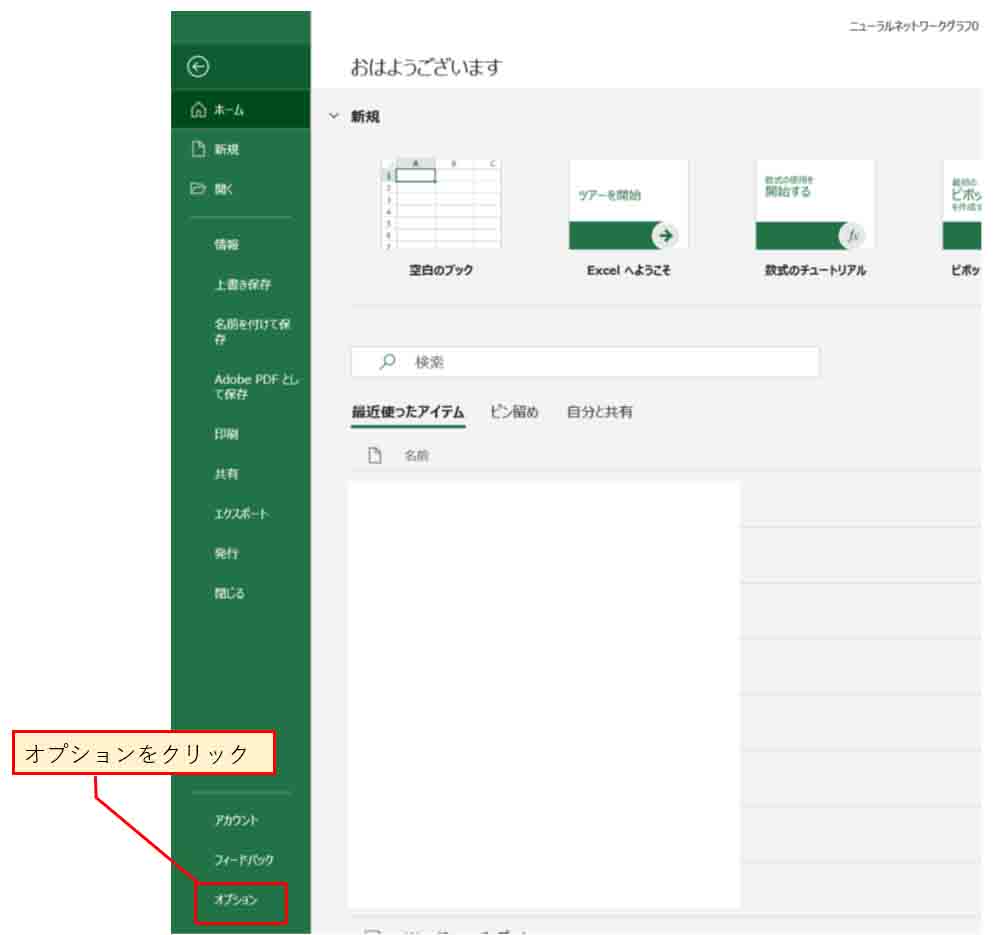
次に、下図の様に「オプション」をクリック。

（図3_02）

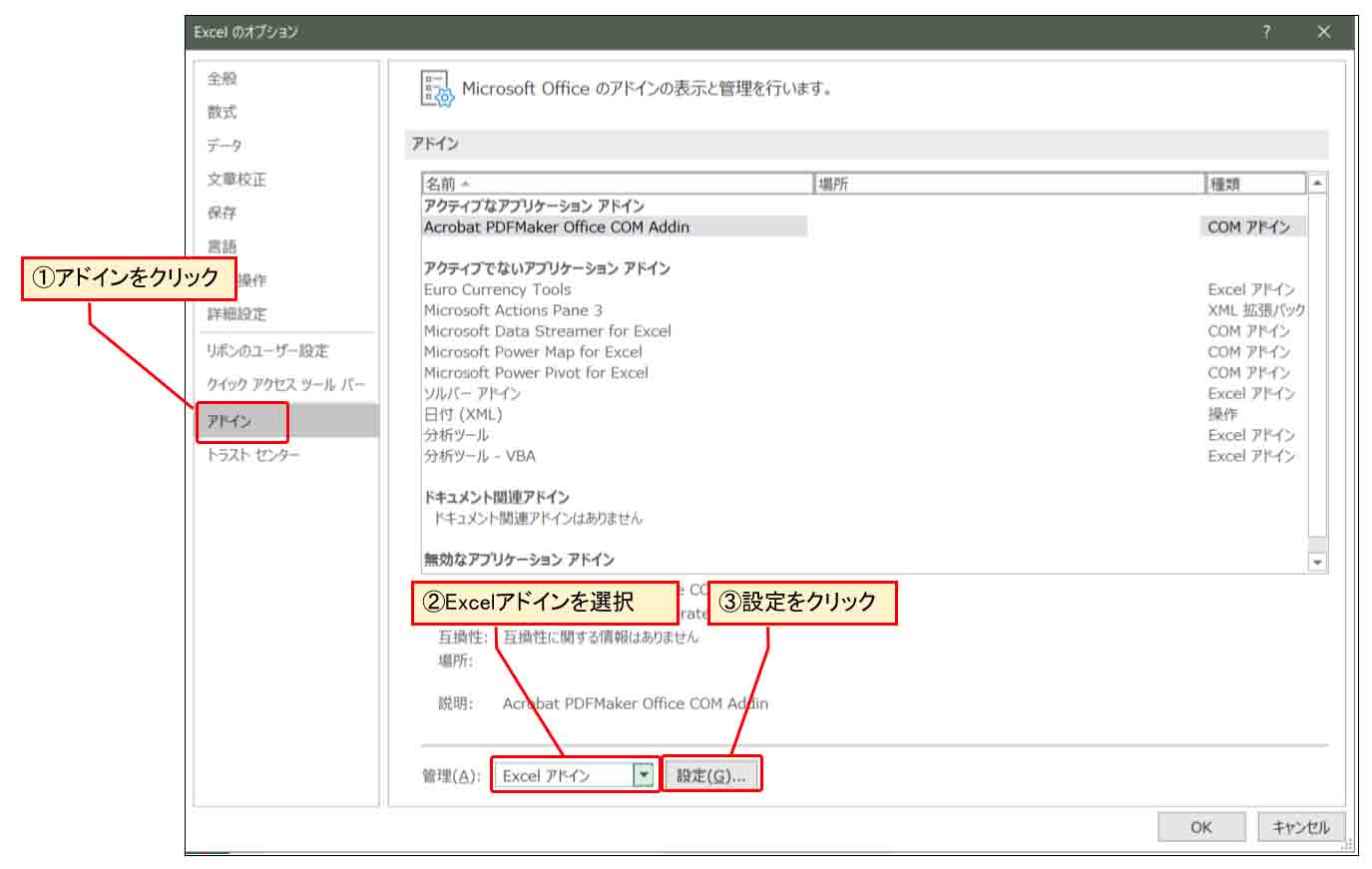
次に、下図の様に「アドイン」を選択し、「Excelアドイン」を選択、「設定」をクリック。

（図3_03）

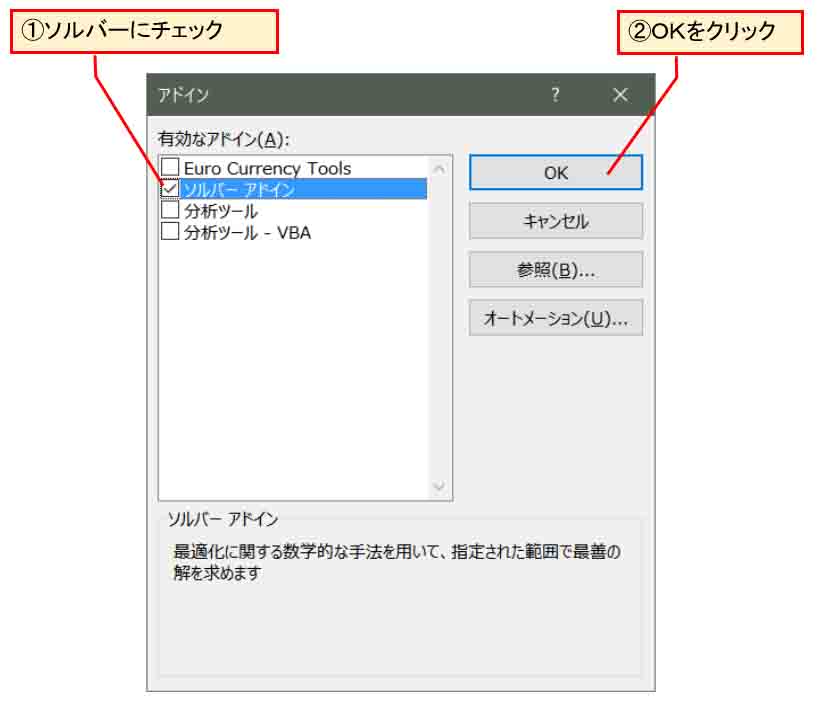
すると、下図の様な画面が出るので、「ソルバーアドイン」にチェックを入れ、ＯＫをクリック。

（図3_04）

以上で、アドインのソルバーインストール完了です。
簡単ですね。

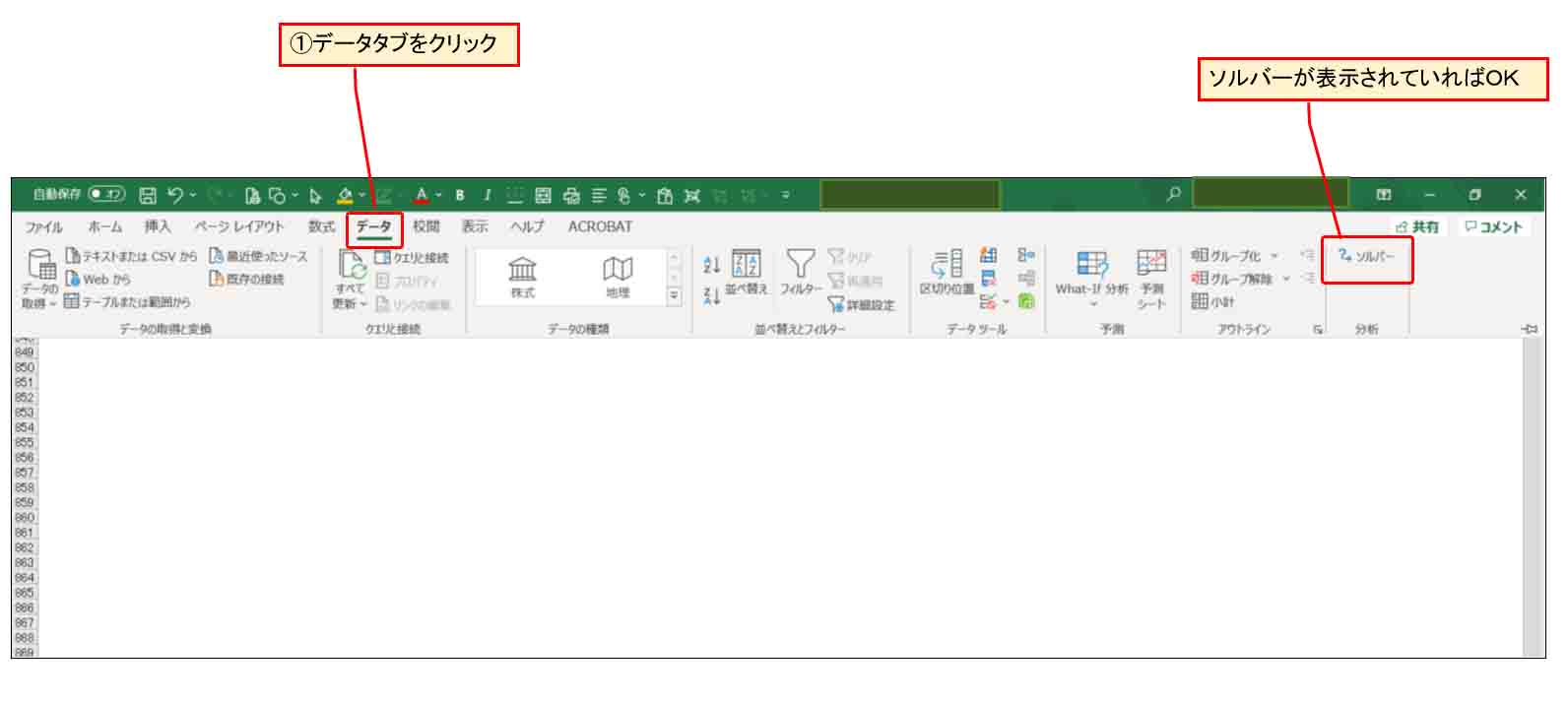
すると、Excel画面の「データ」タブに下図の様にソルバーが表示されていればＯＫです。

（図3_05）

ソルバーで重みとバイアス値の最適解を自動計算させてみる

では、先ほど乱数で入力した出力層の重みとバイアス値から、ソルバーを使って最適解（実際は極小解）を自動計算させてみます。

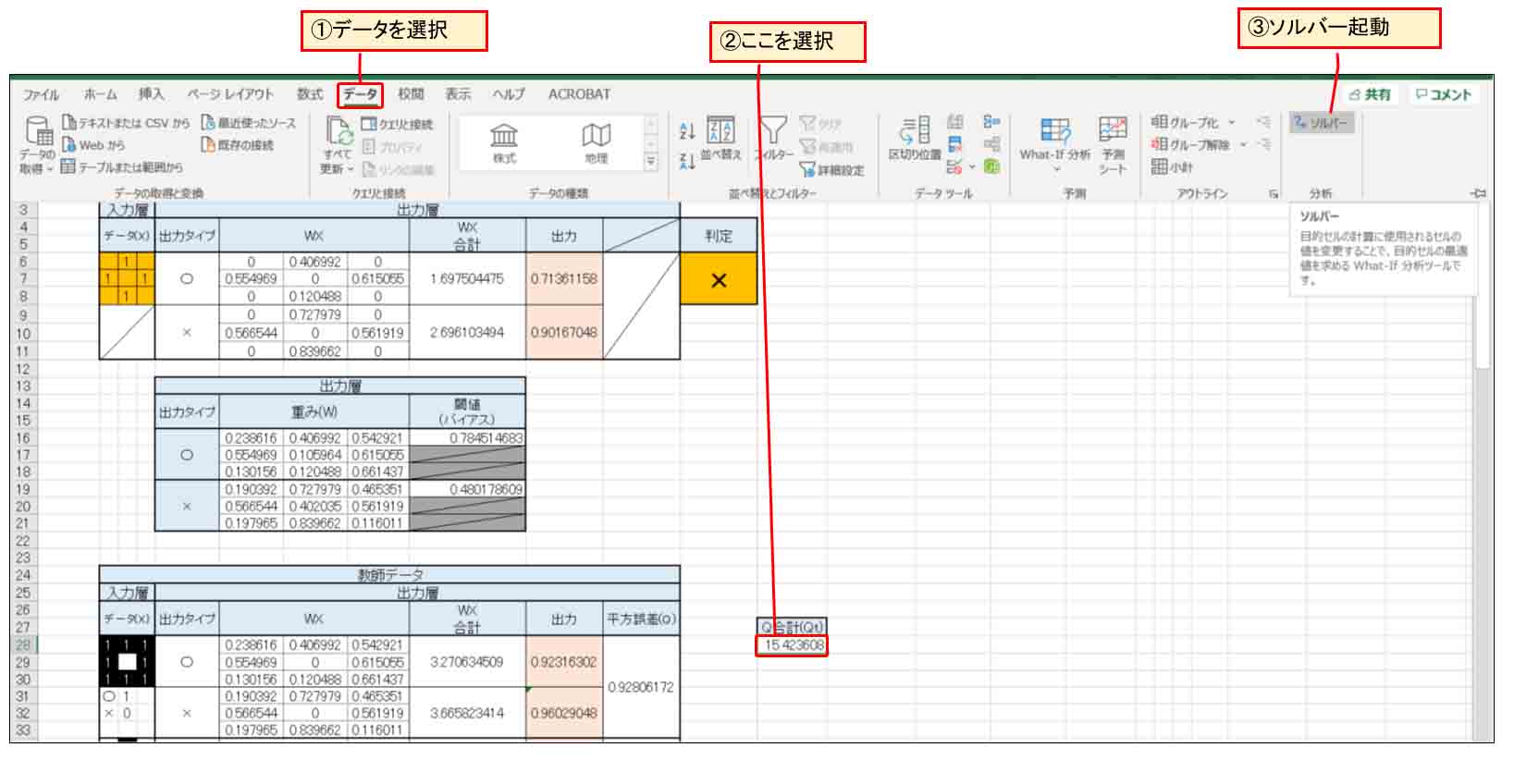
下図の様に、平方誤差Ｑの合計値（Ｑｔ）のセルを選択しておき、ソルバーを起動します。

（図3_06）

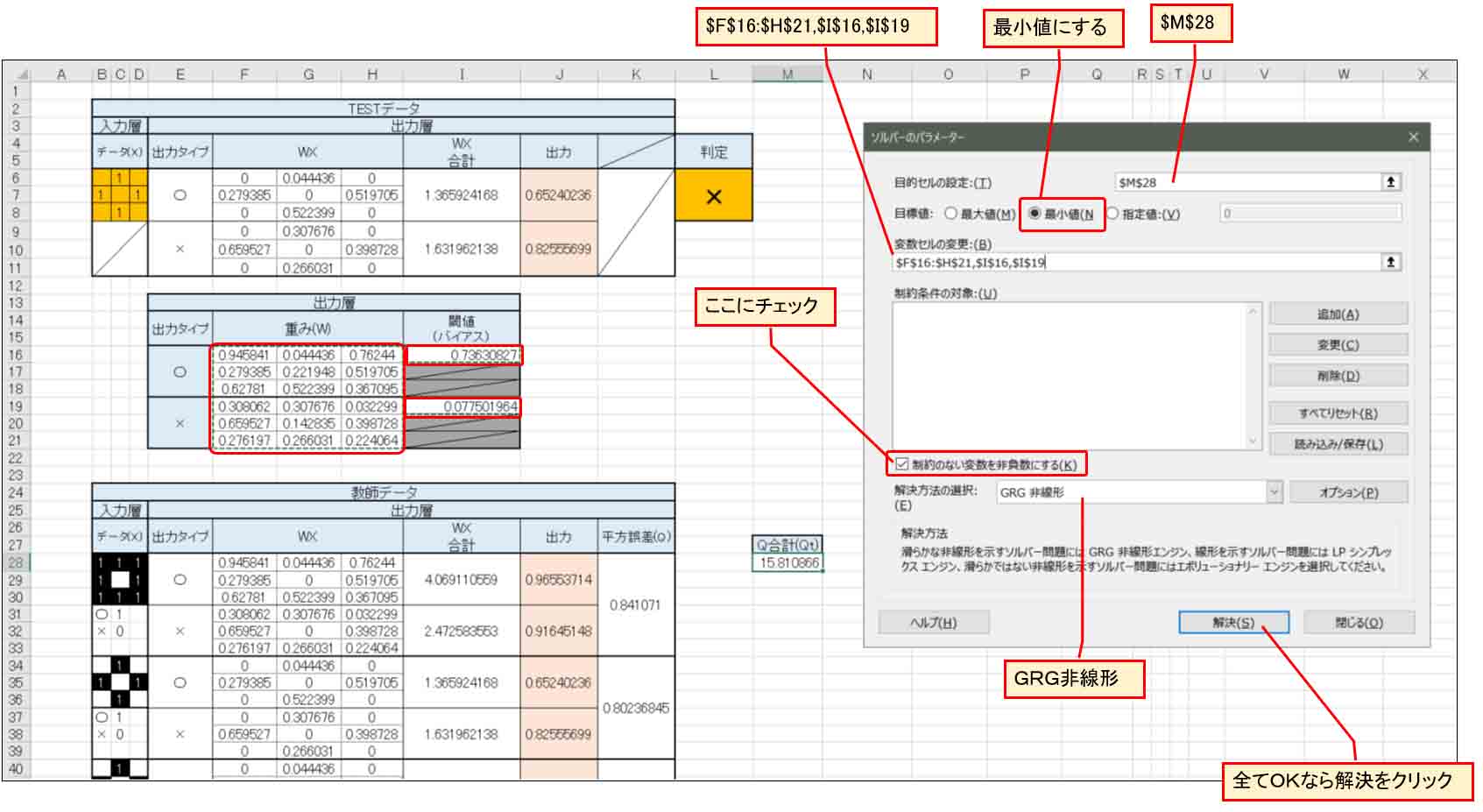
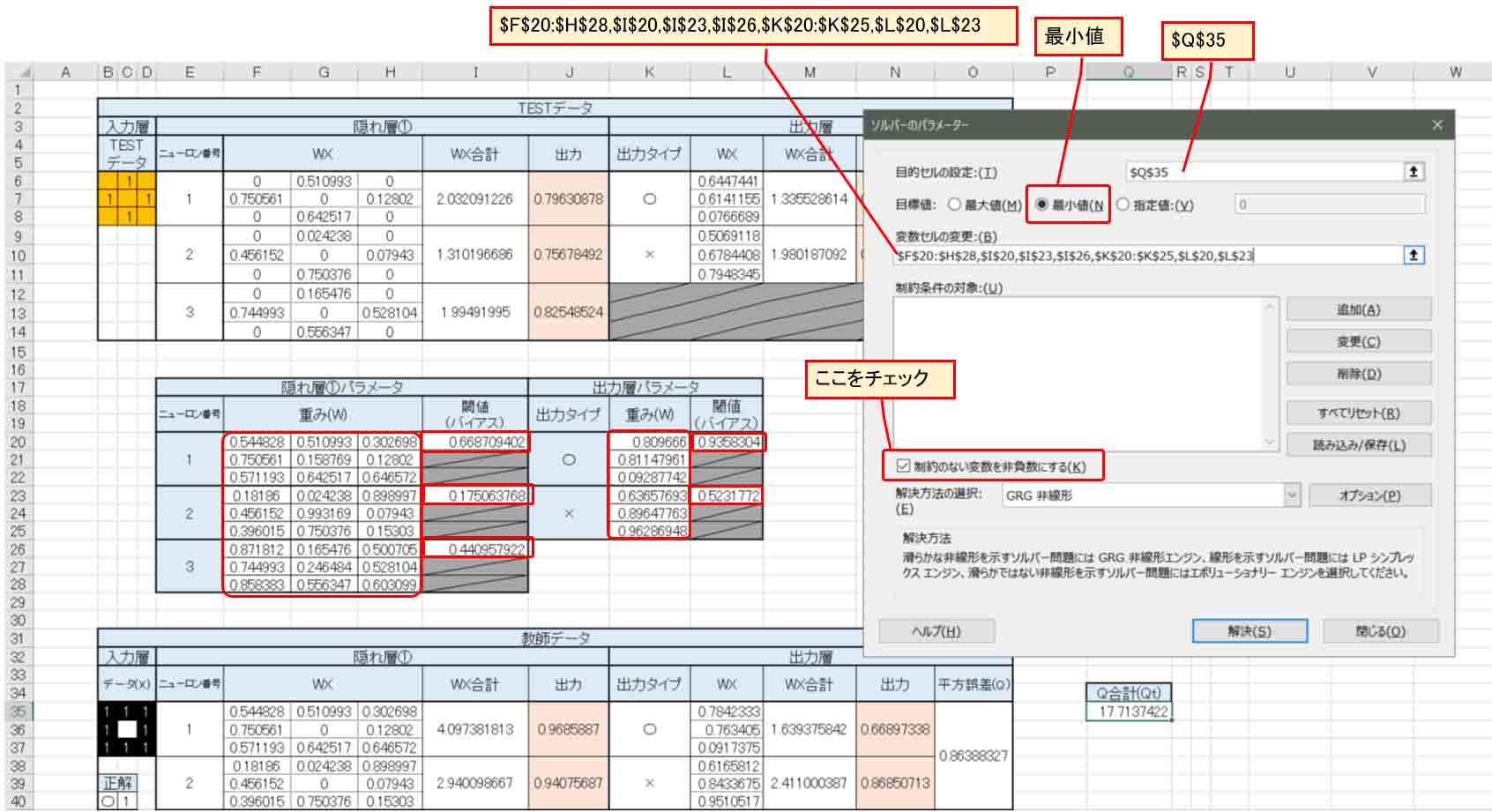
すると、下図の様な画面が表示されるので、参考書籍「Excelでわかるディープラーニング超入門」に習って、下図の様に入力していきます。

（図3_07）

「目的セルの設定」が平方誤差合計（Ｑｔ）のセルです。

「変数セルの変更」は、上図の様に赤枠で囲った部分の出力層の重みとバイアス（閾値）を範囲選択します。
重みはドラック＆ドロップで囲い、その後Ctrlキーを押しながらバイアス（閾値）をクリックすると参照セルを選べると思います。
実際はこんな入力になると思います。

$F$16:$H$21,$I$16,$I$19

そして、「目標値」は「最小値」を選択。
「制約のない変数を非負数にする」にチェックを入れます。

「解決方法の選択」は「ＧＲＧ非線形」を選択して、「解決」ボタンをクリックします。

すると、最適解（実際は極小解）を自動計算してくれて、重みとバイアス（閾値）の値が乱数から最適解に自動的に入れ替えてくれます。

すると、下図の様な結果になりました。

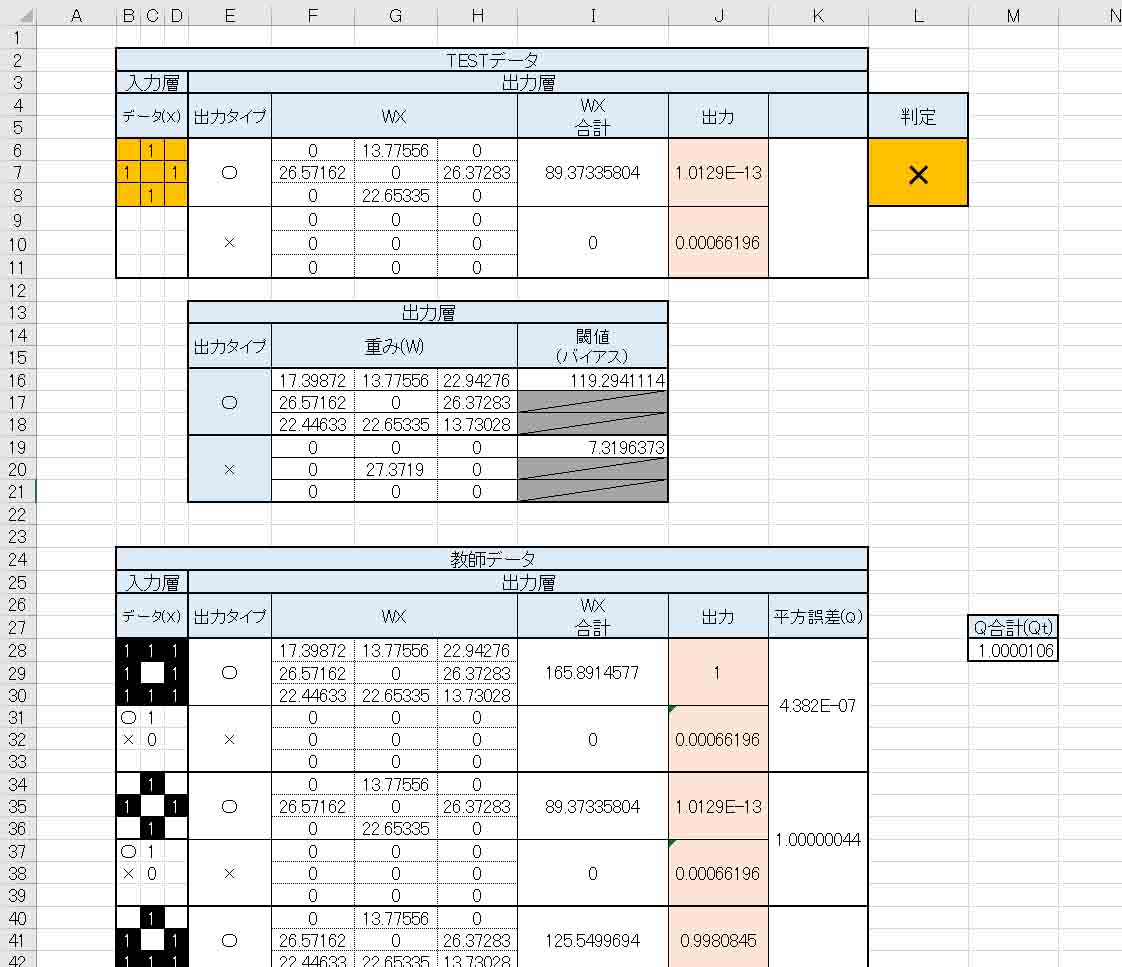
（図3_08）

これは、先ほど述べたように、前回記事の（図3_01）の教師データの場合です。

見て分かる通り、平方誤差の合計（Ｑｔ）の最小値が約1.0と導き出されて、それに対する出力層の重み（Ｗ）とバイアス（閾値）が導き出されました。

重みに関しては、予想通り中央の値が○印の場合はゼロで、×印の場合は重みが高い値でした。

ただし、TESTデータを上図の様に入力してみると、×と判定されてしまいました。
教師データでは○印としているはずです。

考えてみれば、このような
入力層→出力層
という短絡的なニューラルネットワークでは、前回記事の自己流計算式とあまり大きな違いが無いので、結果が悪いのは当たり前と言えば当たり前だなと思いました。

ここで、もう一度、重みとバイアス（閾値）に乱数を入力し、ソルバーで再計算させてみると、下図のようになりました。

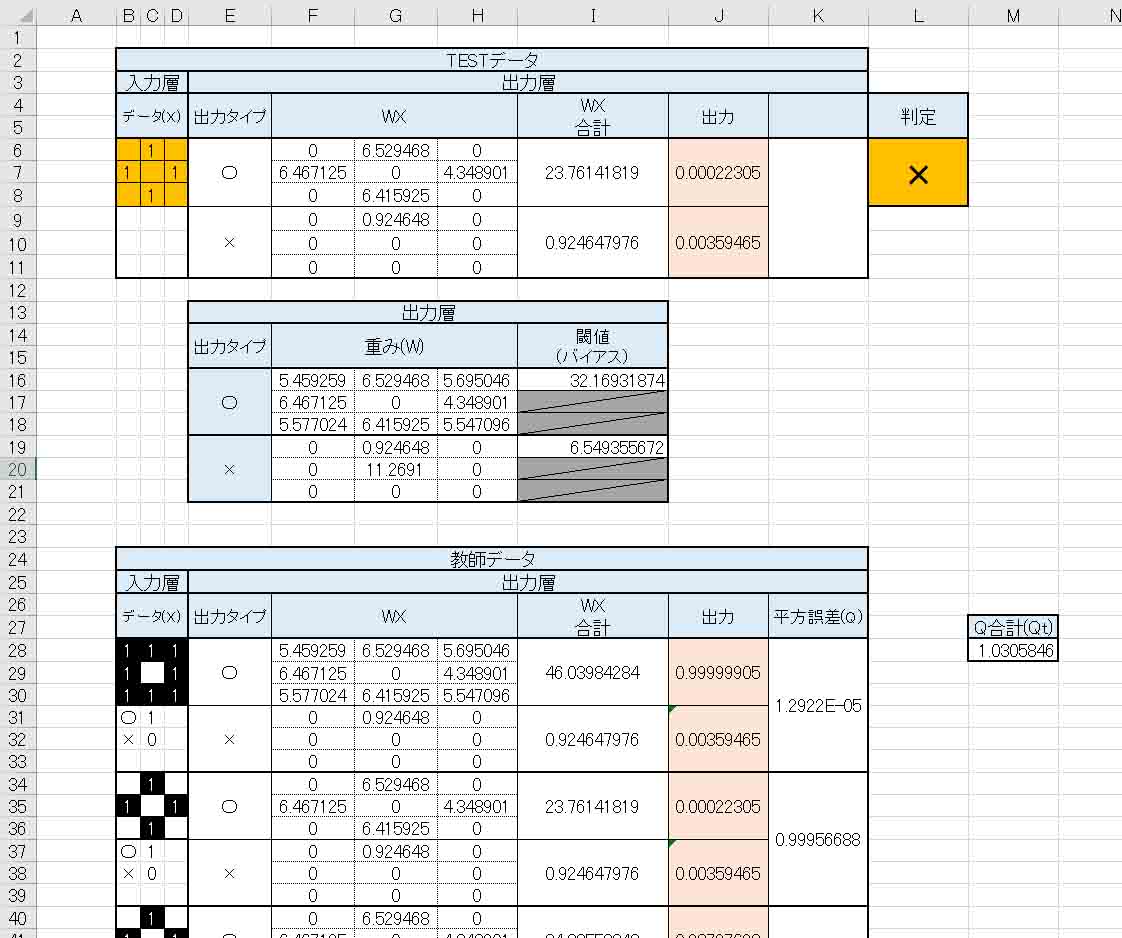
（図3_09）

（図3_08）とは異なる重みとバイアス値になりました。
しかし、TESTデータの判定は変わりありません。

要するに、与えた重みの初期値によって、ソルバー計算の結果が変わって来るというわけです。
これは、参考書籍「Excelでわかるディープラーニング超入門」にも書いてある通り、人間のニューロンのようにその時々で値が変わるのは、ニューラルネットワークの特徴だという意味が分かる気がしました。

そして、重要なのが、先ほども述べたように何度も言いますが、これはあくまで極小解であるということです。
予め入力していた重み（Ｗ）やバイアスデータの値によって、ソルバー自動計算のスタート位置が異なるのです。
値を変えてソルバー計算スタートさせれば、その都度極小解が異なるのです。

４．教師データを追加すると、あら不思議

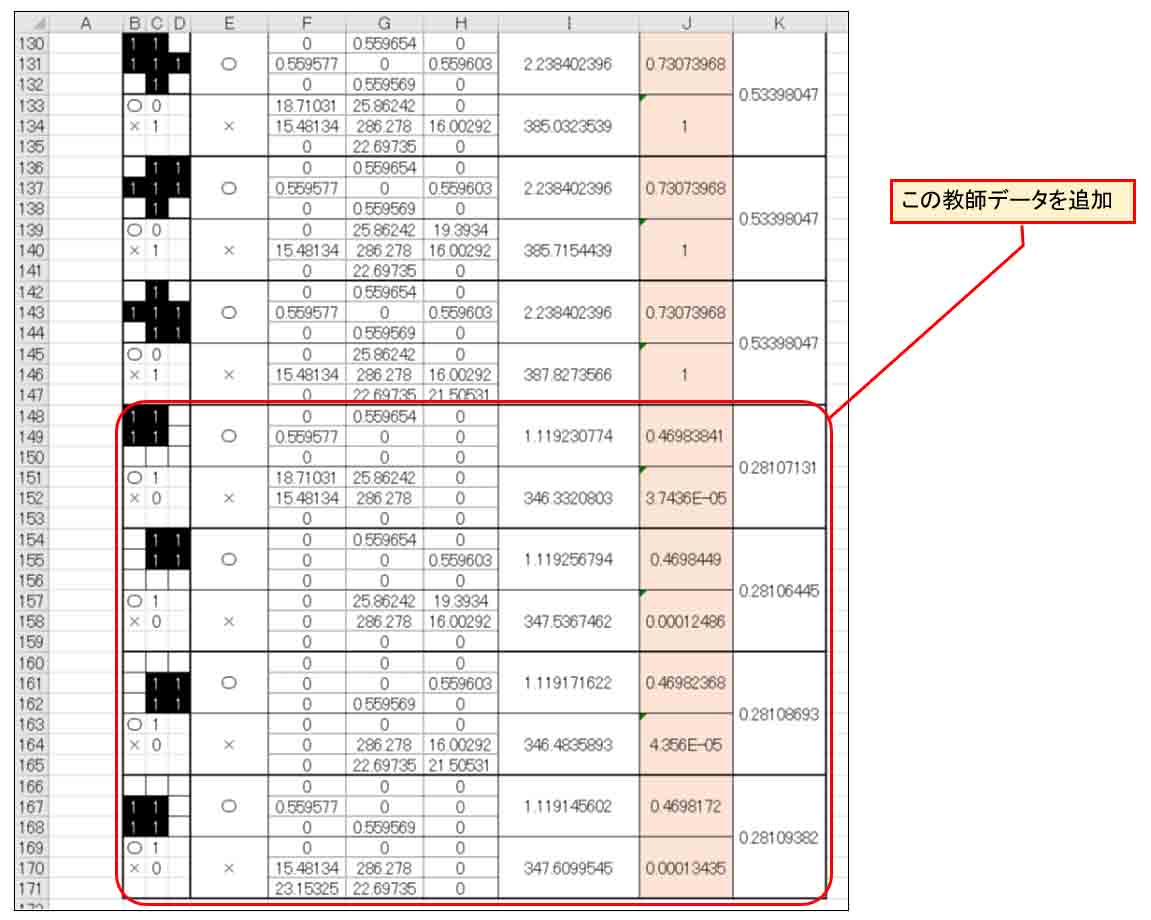
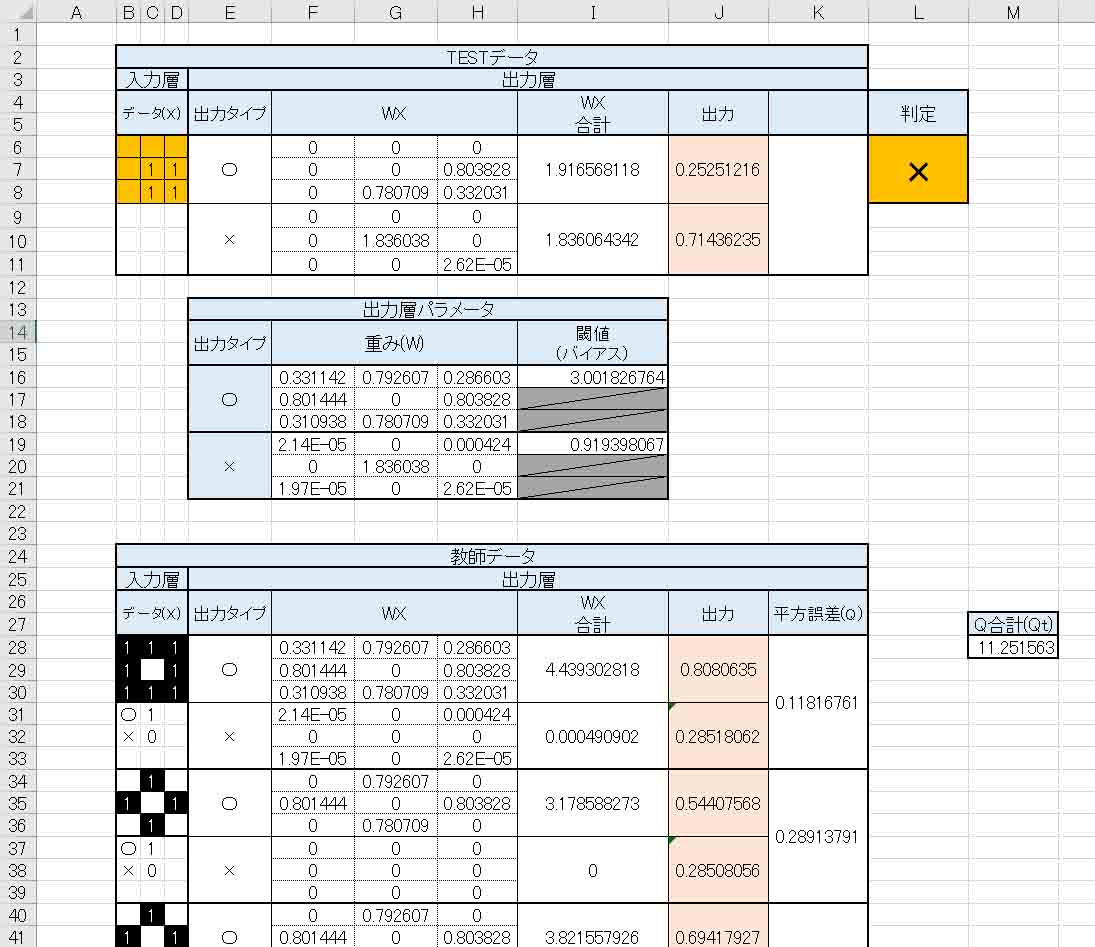
さて、では、今度は下図の様に４パターンの○印としての教師データを追加して、平方誤差の合計（Qt）の範囲も変えます。

（図4_01）

この４パターンは○印なのに中央の画素が入っているという、判定が難しいものになります。
前回記事で紹介したように、普通にプログラミングするならIF文等で条件分岐する必要があるやつですね。

では、平方誤差合計(Qt)のセル範囲を変更し、３章で紹介したように再び重み(W)とバイアス値に乱数を入力し、平方誤差の合計(Qt)に対してソルバーで最適解（実際は極小解）を計算させます。
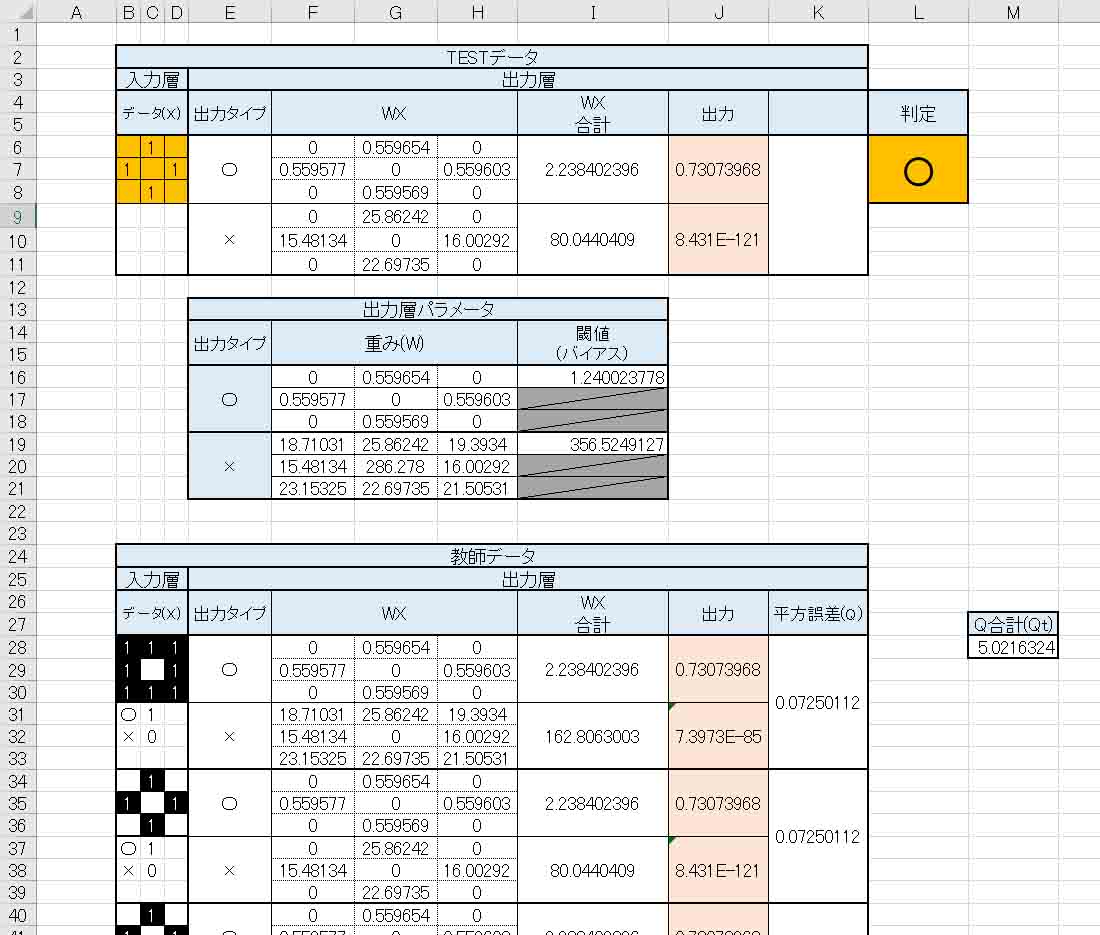
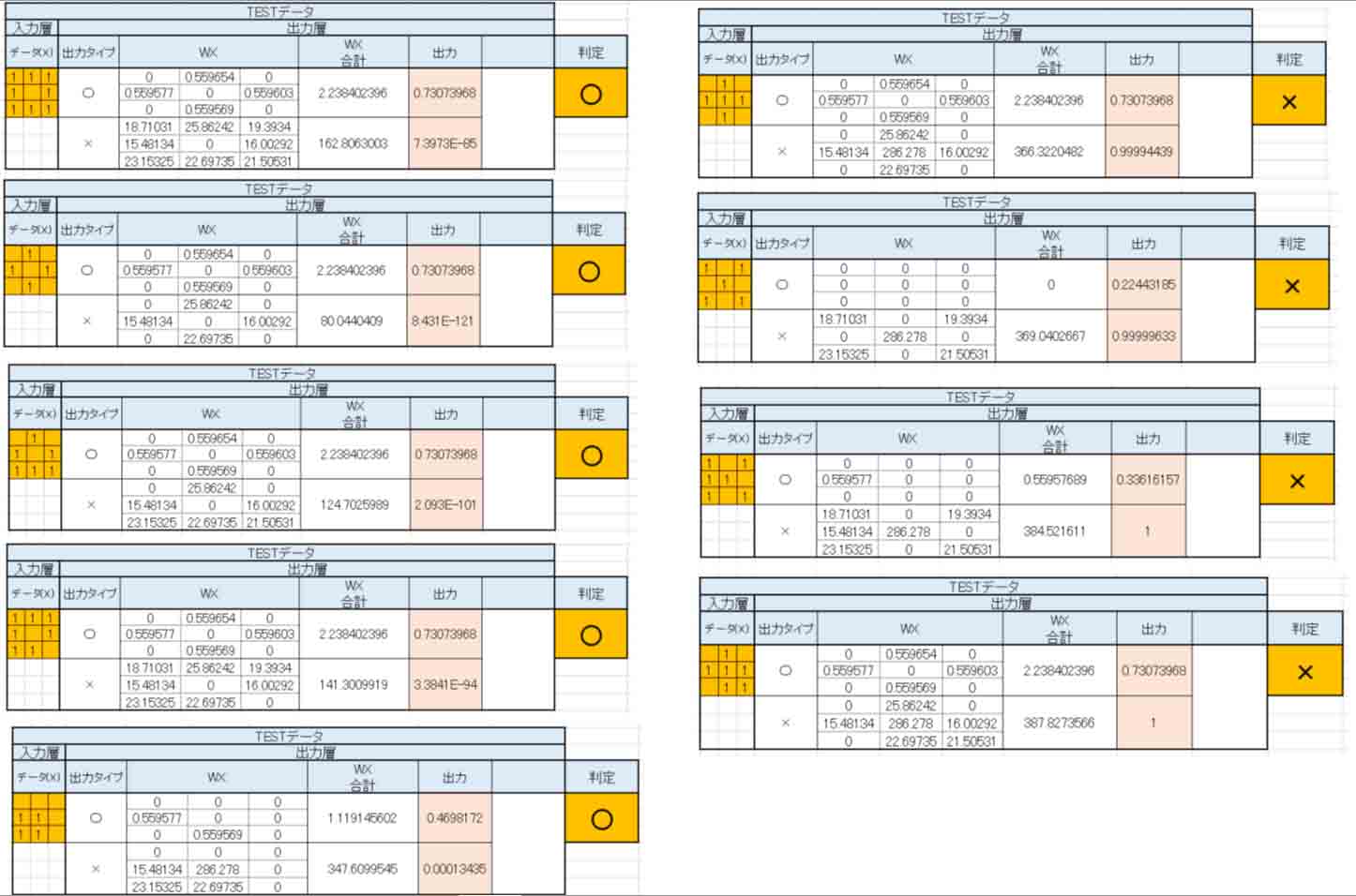
すると、判定結果はこうなりました。

（図4_02）

なんと、見事に判定結果が正常に判定してくれました。
しかも、全ての教師データをTESTデータに入力してみたら、全て正解でした。
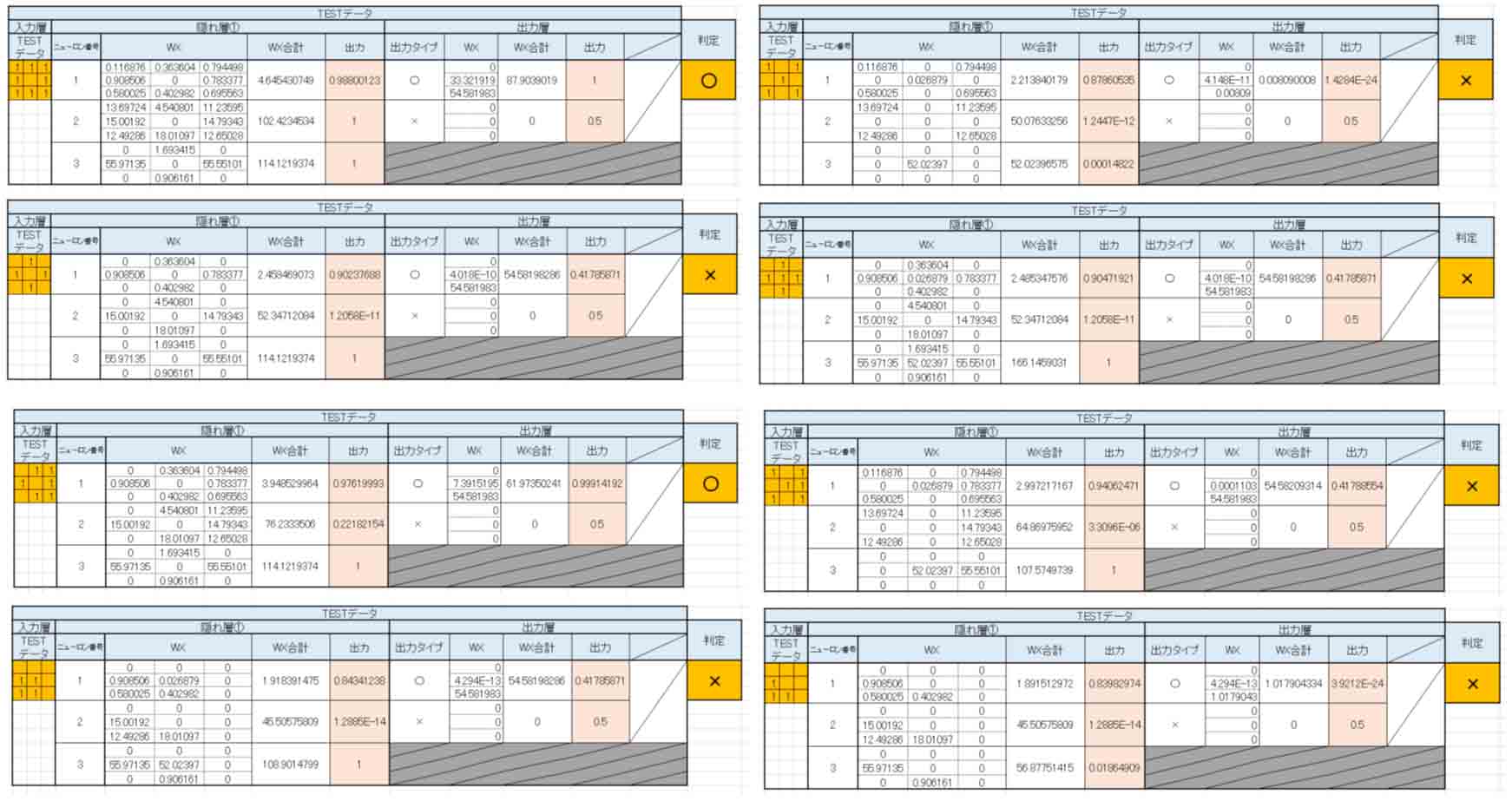
抜粋して見てみると、こんな感じです。

（図4_03）

お見事！！！

前回記事の様な変なIF文条件分岐をしなくても、重みとバイアス（閾値）を変えただけで、ここまで正解率がグーンとアップするんです。
（図3_09）と（図3_11）の重み（Ｗ）とバイアス（閾値）を見比べてみると、（図3_11）では重みが全画素に値が入力されています。

これは何とも不思議ですね。
このExcel表は複雑な計算式は一切無く、重みとバイアス値の微妙な数値が重大な役割を担っているということが体感できますね。
今まで独学で４～５年プログラミングしてきて、ちょっと驚きでした。

以上から、これこそがニューラルネットワークとディープラーニングの大きな特徴だと言えそうな気がしてきました。
だんだんと通常のプログラミングとディープラーニングの違いが分かって来ましたね。

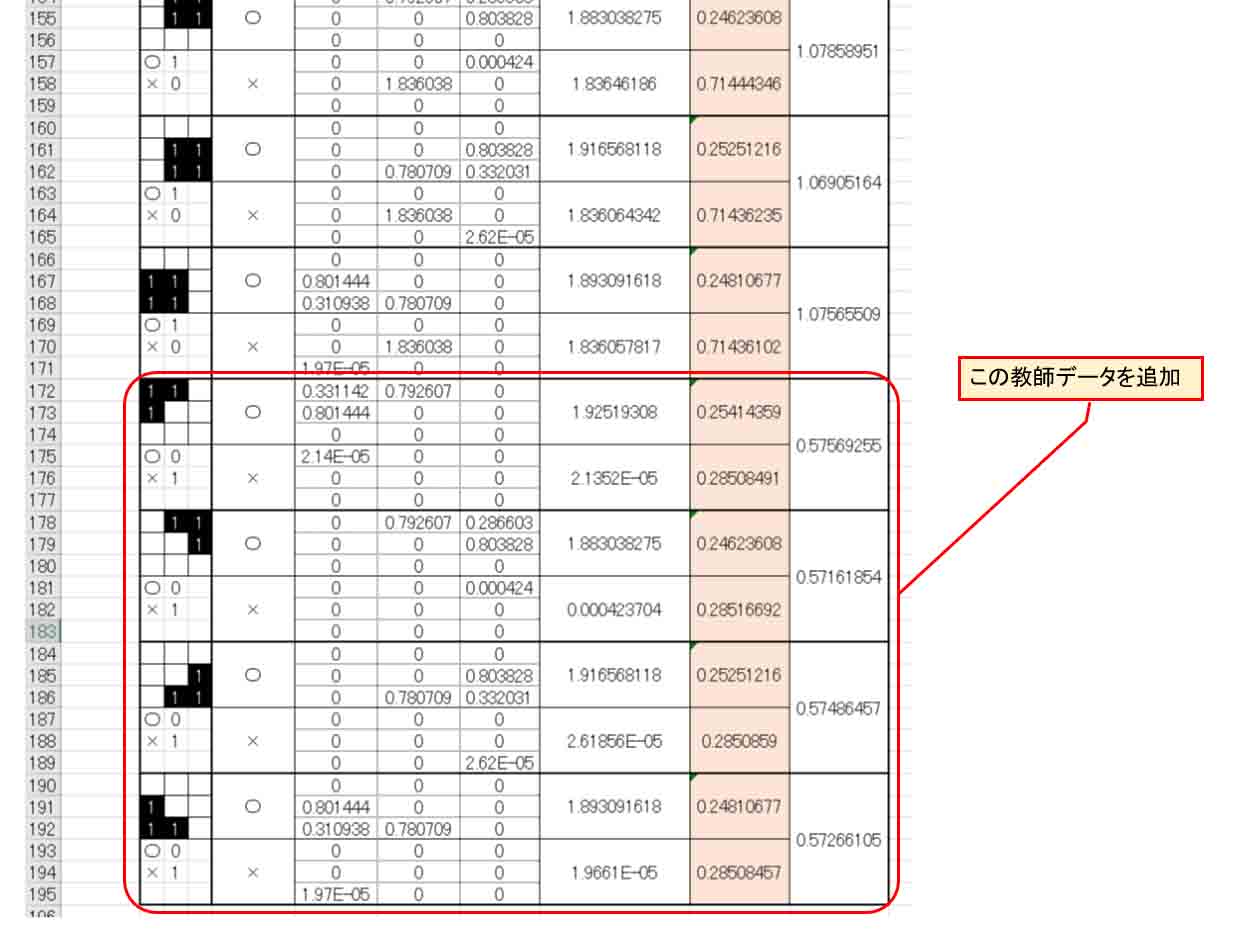
では、今度は、もっと混乱しやすいデータを追加してみたいと思います。
○印としての教師データと競合しそうな微妙な×印としての教師データを追加してみます。
下図の様な感じです。

（図4_04）

これは、カメラに×印の端の部分だけ映し出されている場合と思って下さい。
そして、中央の画素が0です。
中央のデータが0の多くは○印としてのデータです。
これは機械学習としては難しくなりそうなので、あえて混乱させてみるとどうなるのでしょうか？

では、平方誤差合計(Qt)のセル範囲を変更して、重み（Ｗ）とバイアス（閾値）に乱数を入力し、ソルバーで再計算させます。

すると、こういう判定になりました。

（図4_05）

本来、このデータは○印のはずですが、うまくいきませんね。
重み(W)とバイアス（閾値）をパッと見ても、増えた教師データに対応できていないように見受けられます。
これはおそらく、入力層と出力層だけのニューラルネットワークでは単純さゆえの限界だと思います。
さすがにこんな単純なネットワーク細胞では正常な判断はできないんでしょうね。

ところで、これは第２章のところで述べたように、ソルバーの最小値は極小値であることを頭に入れておかねばなりません。
ですから、乱数によるソルバー解決スタートよりも、ある程度予想して重み(W)とバイアス（閾値）を設定してからソルバーを使うと良い値が導き出されるかもしれません。

いずれにせよ、重み(W)とバイアス値は私の頭では予想ができないブラックボックスなので、最適な値からソルバーをスタートすることができません。
これも恐らくディープラーニングの大きな特徴なのだと思います。
要するに、重みとバイアス値は人間には予想できないブラックボックスなので、ニューラルネットワークの量と深さと教師データの数や種類によって重みとバイアス値は刻々と変化するということのようです。

ならば、ニューラルネットワークに一つ層を増やして、いわゆる「隠れ層」というものを加えるとこれが解決できるのかどうかを、次で実験してみます。

５．ニューラルネットワークの隠れ層を入れてみる

では、いよいよちゃんとしたニューラルネットワークらしく、隠れ層を１つ入れてみます。
最初に紹介した書籍「Excelでわかるディープラーニング超入門」の例に習って、隠れ層のニューロンは３つとします。
つまり、概略図で言うとこんな感じです。

（図5_01）

では、重みとバイアス（閾値）に乱数を入力して、Excelで組んでみると、こんな感じです。

（図5_02）

隠れ層が追加されると、途端に複雑になったように見えますが、実際のところ作ってみると意外と簡単でした。
教師データは、（図4_04）までのデータと同じです。

そして、TESTデータ部分も教師データからコピーして以下のように作っておきます。

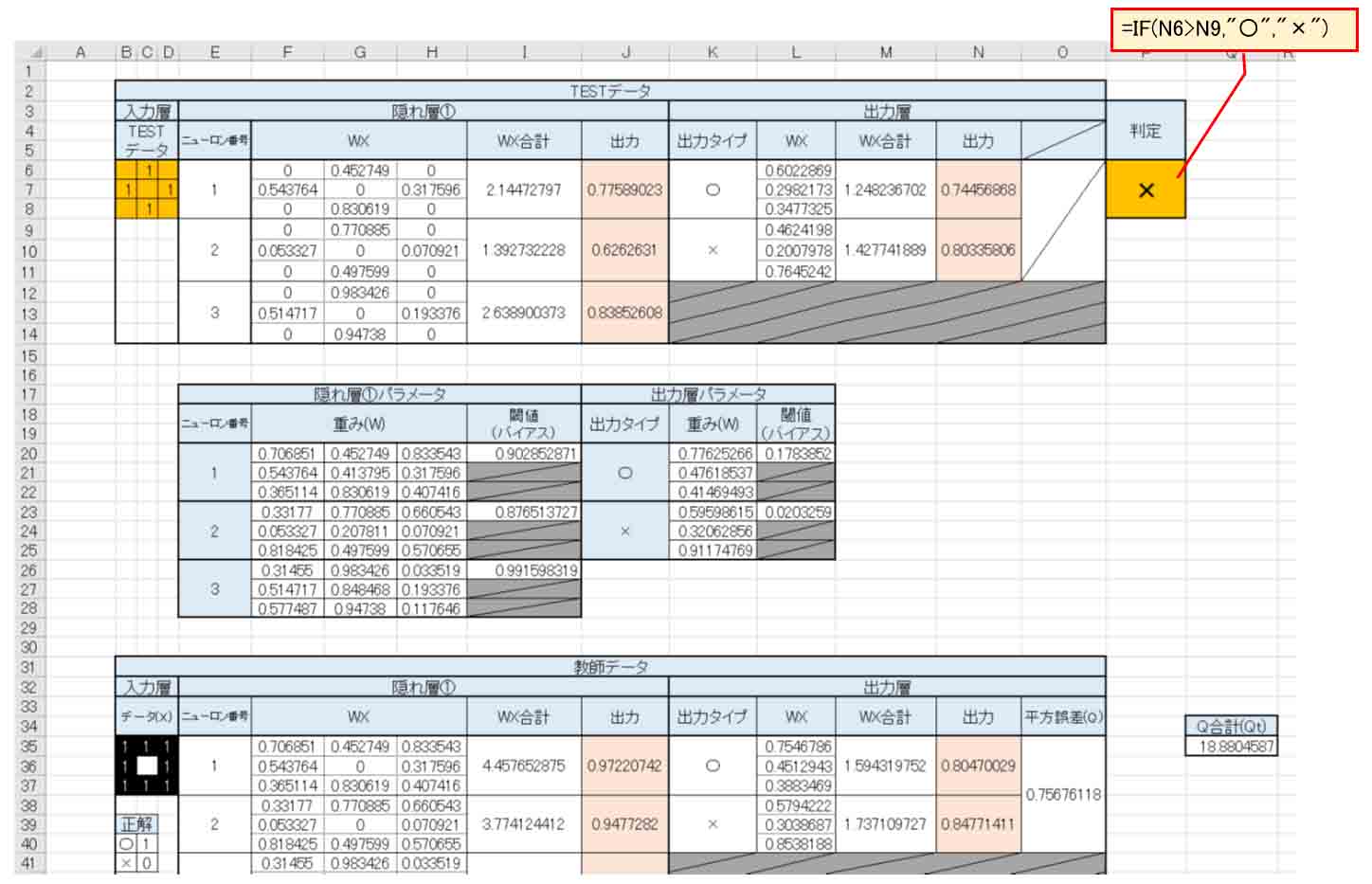
（図5_03）

では、前で述べたのと同じようにソルバーを使って、重み(W)とバイアス値を乱数から最適解（実際は極小解）にしてみます。
以下の感じです。

（図5_04）

では、解決をクリックしてみます。
すると、以前より計算に時間がかかっていることが分かると思います。
やはり、ネットワークが増えると計算量が増えて時間がかかるのはあたりまえですね。

重み(W)とバイアス（閾値）はこんな感じになりました。

（図5_05）

あれ？
出力層の×印の重みとバイアスがゼロになってしまいました。
これでいいのかな？

主な結果はこんな感じです。

（図5_06）

見ての通り、8テスト中、２つも間違えています。
あれ？
期待していた精度が出ていませんね。
隠れ層を追加したにもかかわらず、結果が悪くなりました。

これはもしかしたら、２章で述べたように、ソルバーが極小解しか導き出せないところに原因があるかも知れません。
もうちょっと最適な値からソルバーをスタートしたら別の更なる最小解が見つかって、もっと良い結果が得られるかもしれません。
でも、良さげな重み(W)のスタート値が全くの不明なので、これより良い結果を得ることは無理です。

ならば、４章で実験したように、教師データを増やすと良い結果が得られるかもしれません。
下図の様に×印としてのデータを追加してみます。
これは、カメラで×印の半分を捉えた時のデータです。

（図5_07）

更に下図の×印としてのデータも追加します。

（図5_08）

そして、○印としてもカメラで半分を捉えた時のデータを追加してみます。
中央の画素が入っているので、×印との判別が難しくなるデータです。

（図5_09）

ここまでの教師データの数は合計４０個になりました。

では、平方誤差合計(Qt)の参照範囲を修正し、３章で説明したように重み(W)とバイアスに乱数を入力して、ソルバーで新たに最適解（実際は極小解）を求めてみます。
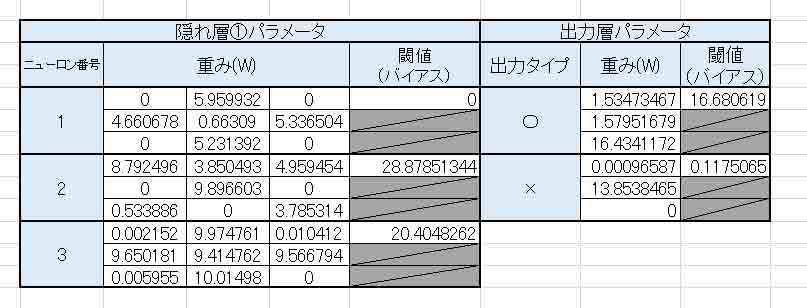
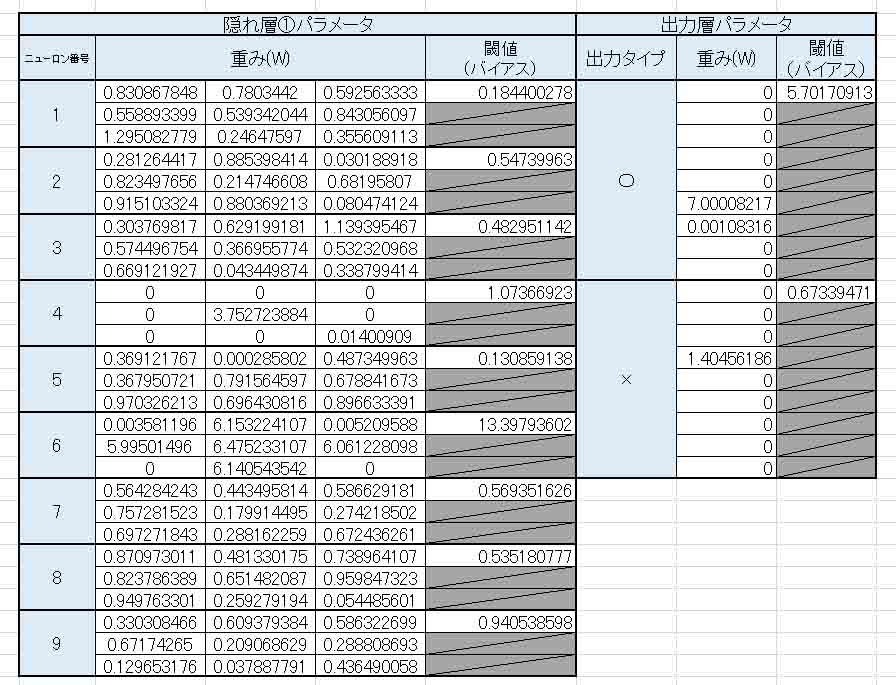
すると、重み(W)とバイアス（閾値）は以下のようになりました。

（図5_10）

先ほどの（図5_05）と違って、出力層の×印の重み(W)にちゃんとデータが入っていますね。
これから分かる通り、教師データの数が多ければ多いほど、データがしっかりしてくると見受けられますね。

では、これをTESTデータでちゃんと正解するか見てみます。
Excelで入力層と判定データだけ抽出して並べてみました。

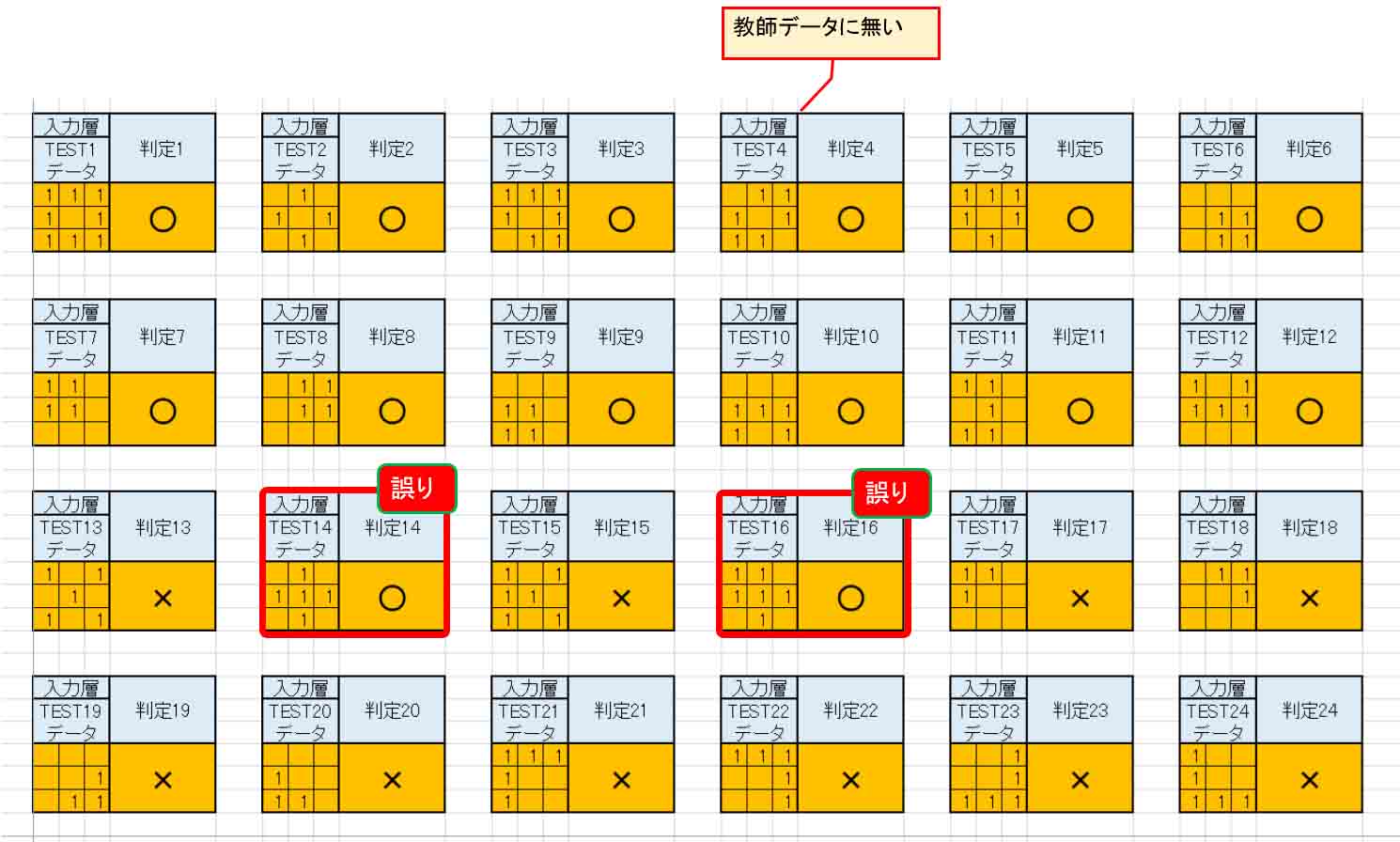
（図5_11）

判定4は教師データに無いのにうまい具合に○印として判定してくれました。

ただ、判定14と判定16が誤りでした。
本来、×印として判定してくれなければなりません。
たった２パターンの誤りですが、それでもこれは正しく判定してくれなければ困ります。
これでは画像認識としては使えないですね。

どうしてこうなるか、（図5_10）をよく見てみると、隠れ層の重み(W)とバイアス（閾値）のデータパターンが少なすぎるために正しく判定できていないような気がします。

ならば、隠れ層のニューロンを増やしてみるとどうなるのかを次で実験してみます。

６．ニューラルネットワークの隠れ層のニューロンを増やしてみる

これまでは隠れ層①のニューロン数は３つでした。
ならば、入力層と同じだけのニューロン数９個に増やしてみるとどうなるかを実験してみます。

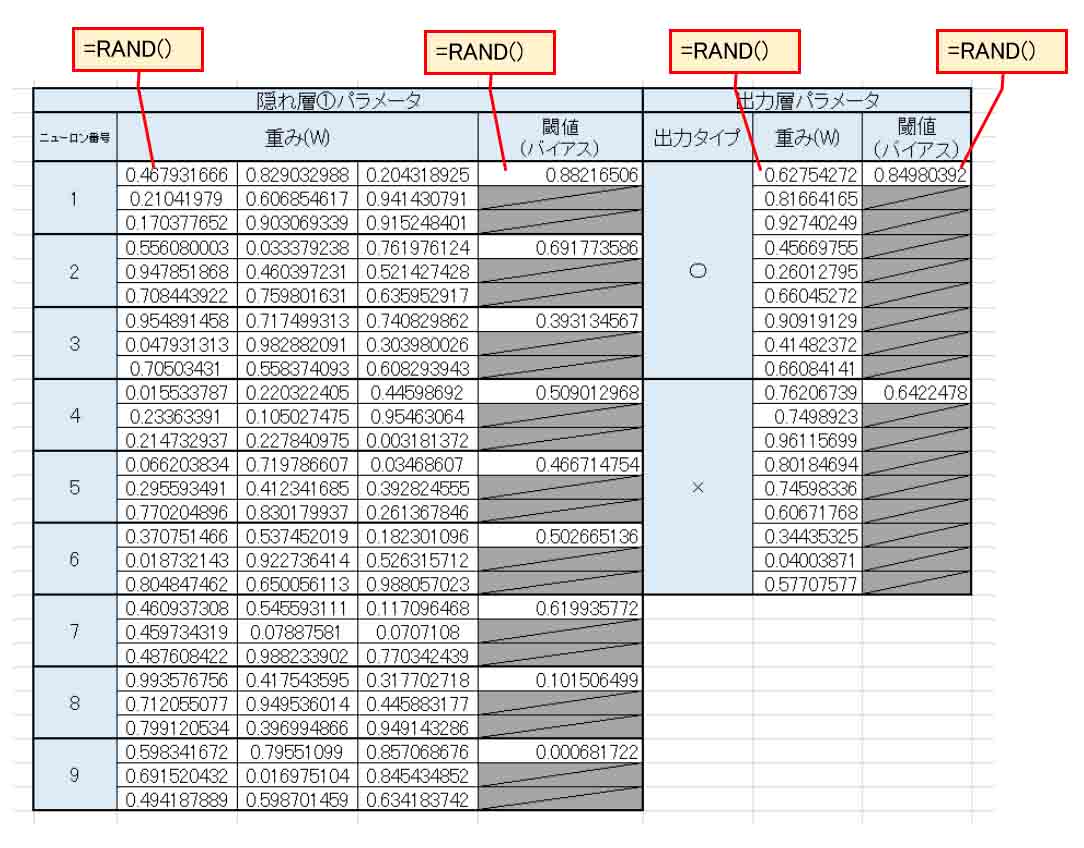
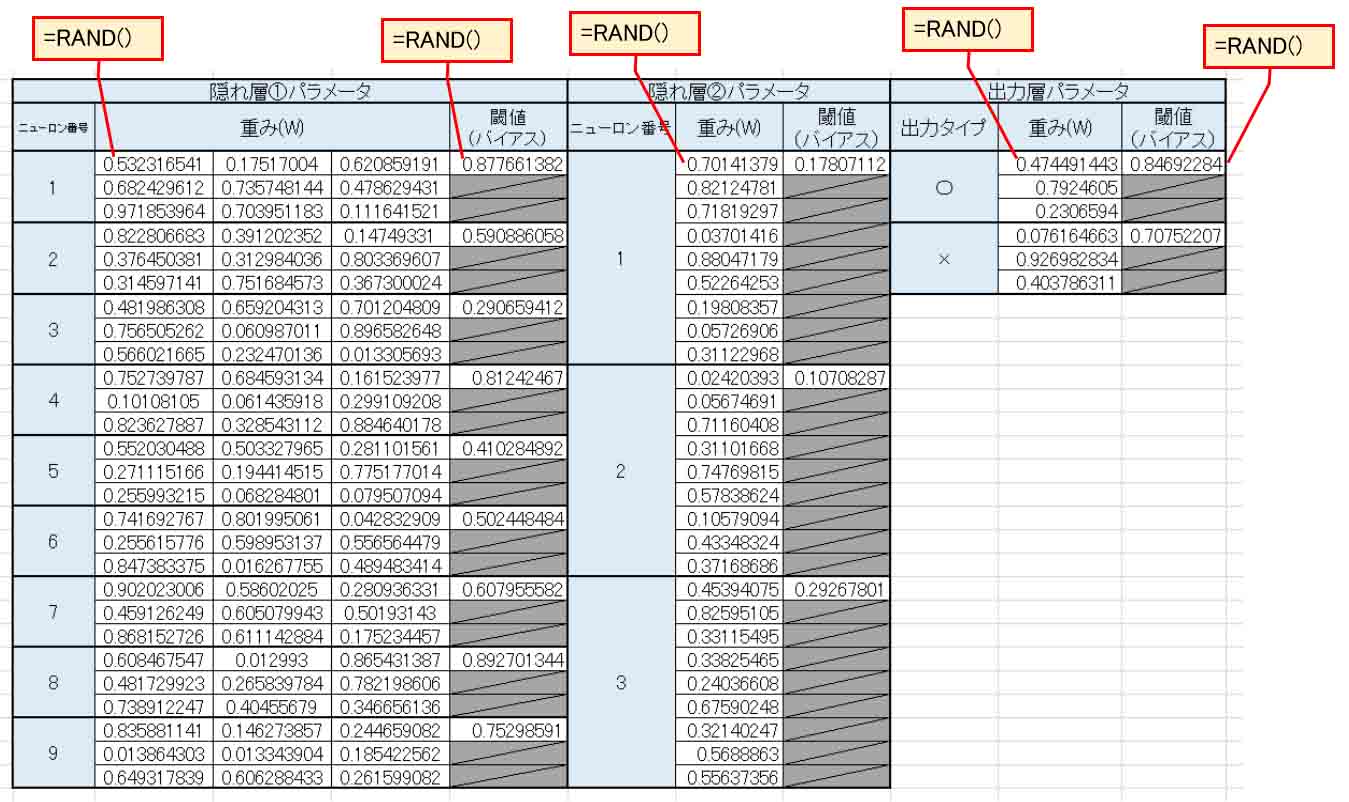
まず、前に述べたように、下図の様に重み(W)とバイアス（閾値）に乱数を入力した表を作って置きます。

（図6_01）

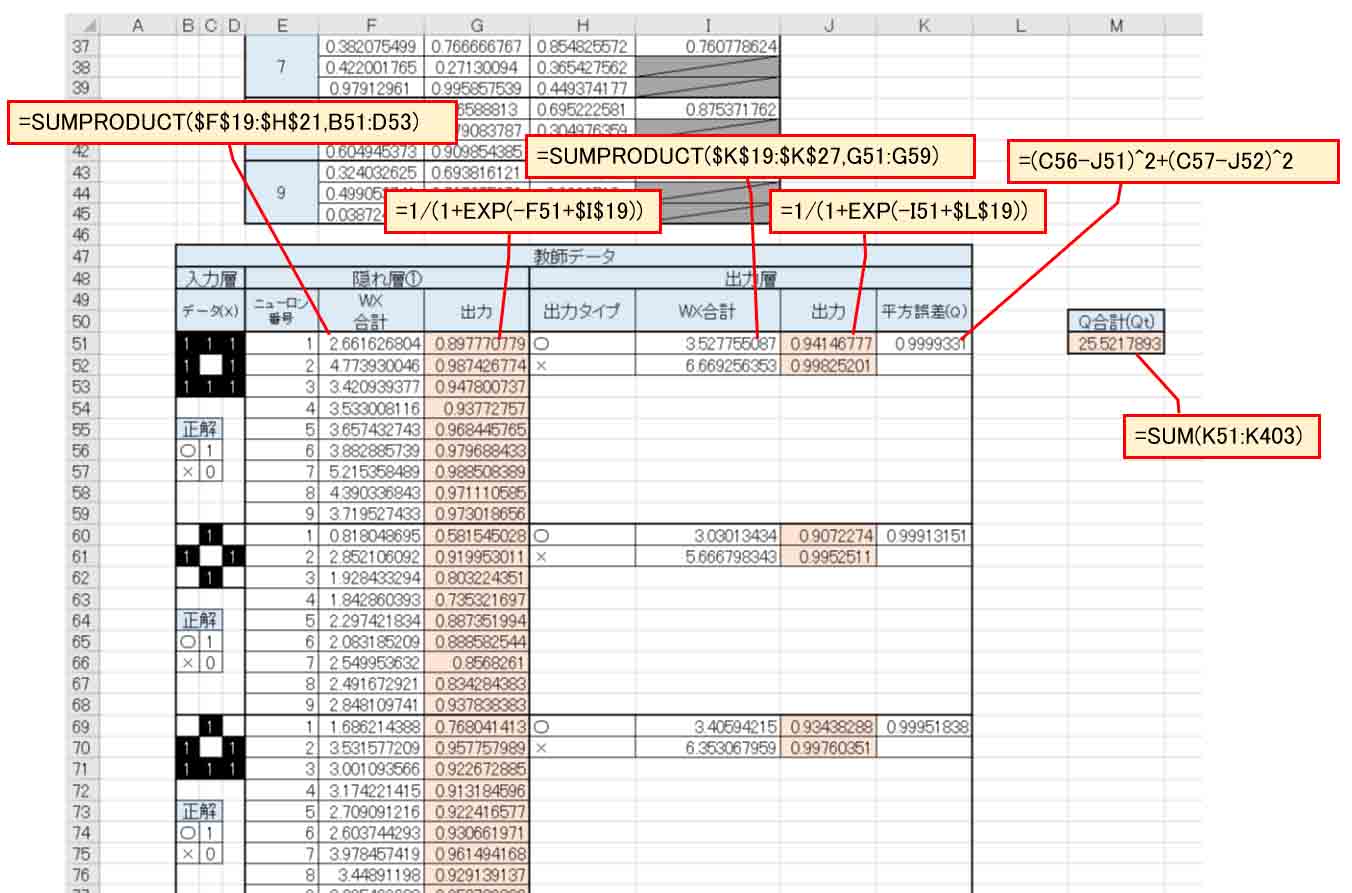
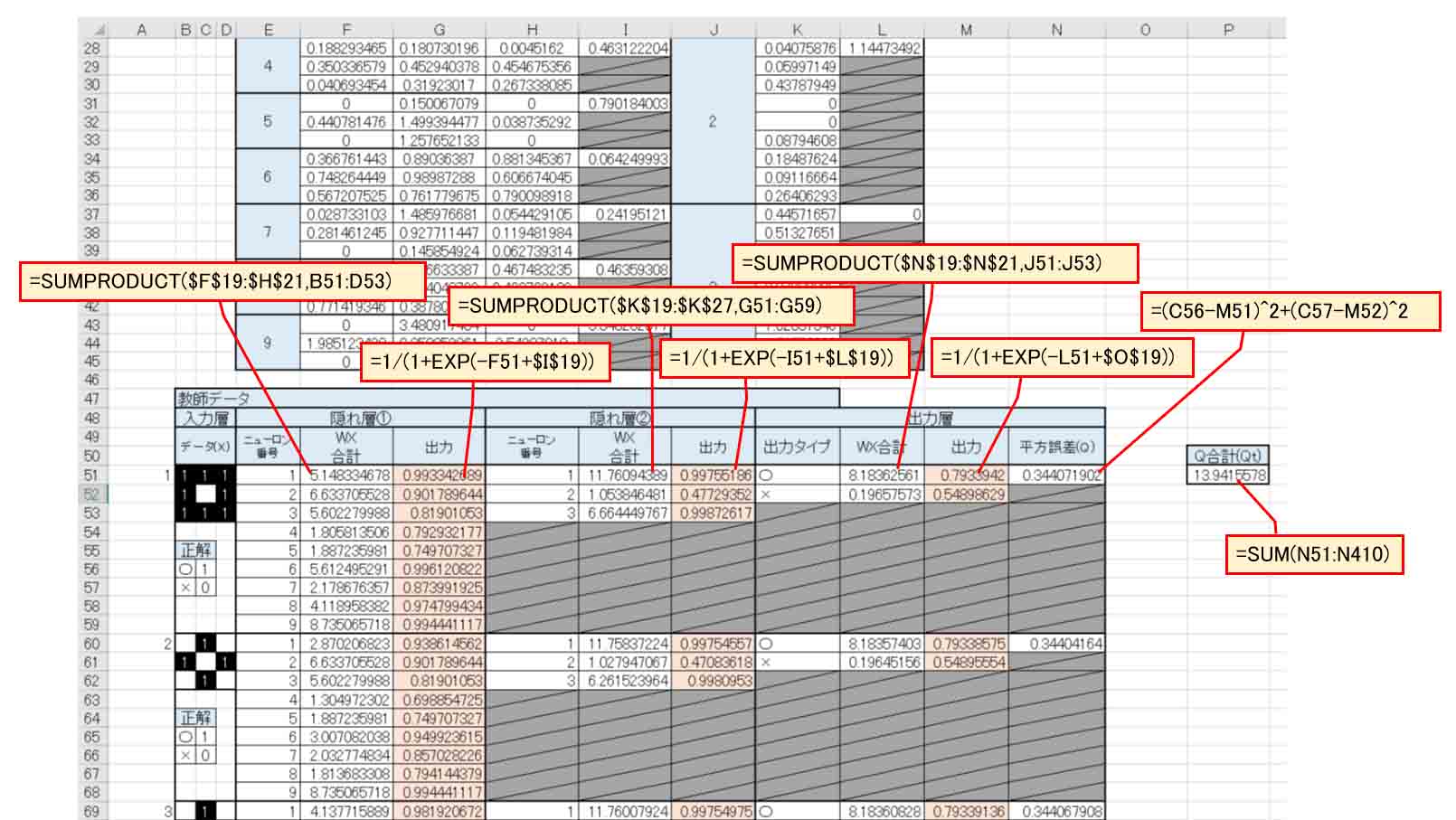
次に下図の様に先ほどと同じ４０種の教師データを入力しておきます。
WX合計はExcelの便利な関数 SUMPRODUCT を使いました。
これを使うと、欄が少なくなって見栄えがスッキリしますね。

（図6_02）

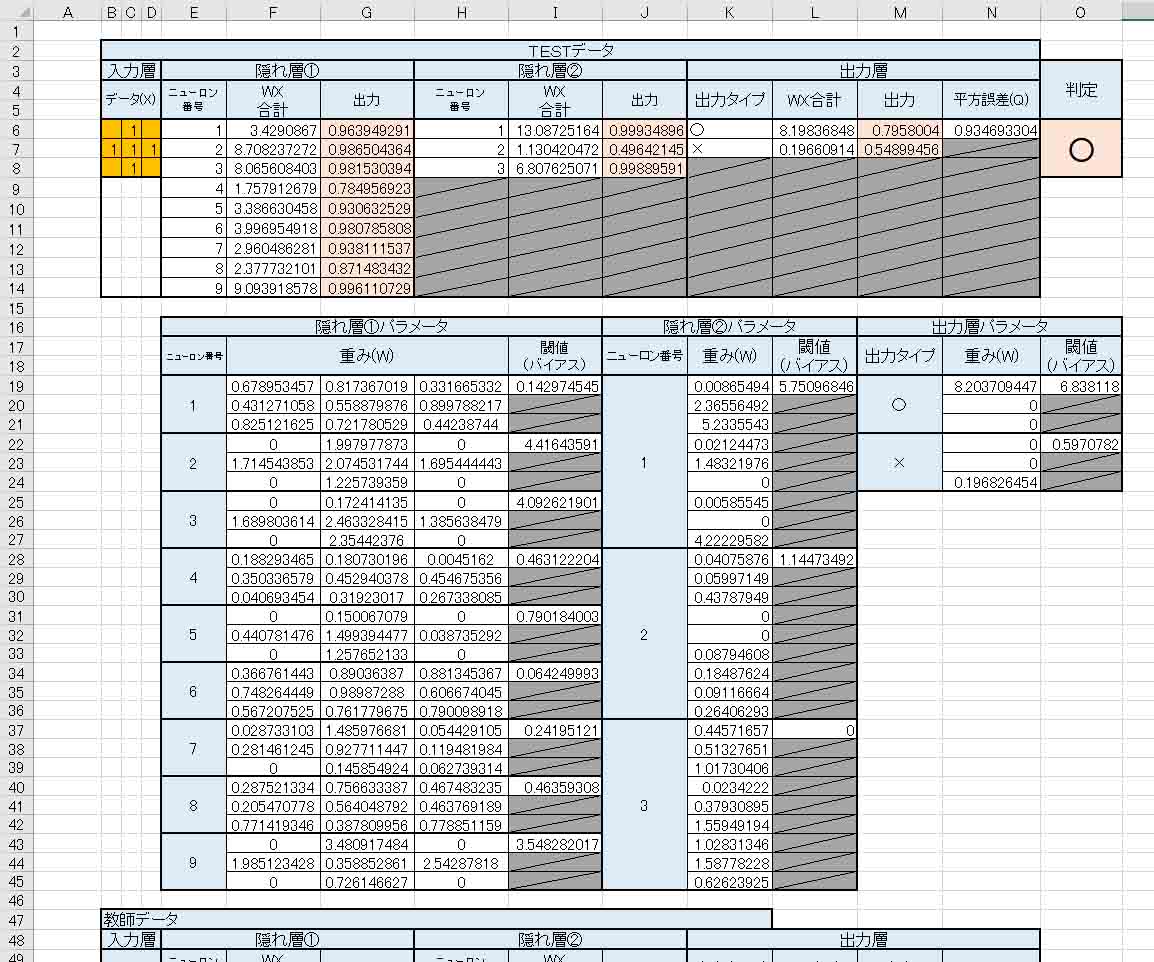
そうしたら、一番上にTESTデータとして教師データからコピーして作って置きます。

（図6_03）

では、３章で述べたように、平方誤差合計値(Qt)が最小になるようにソルバー計算させてみます。
ニューロンが多いので、私のパソコン環境では計算に３８秒かかりました。

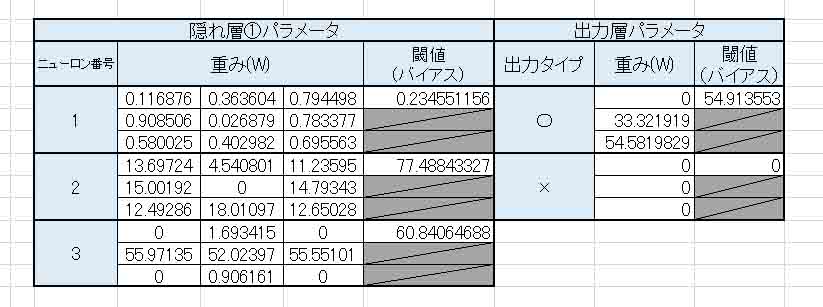
すると、重み(W)とバイアス（閾値）は以下のようになりました。

（図6_04）

これ、何かおかしいですねぇ。

特に出力層の重み(W)を見ると、0がやたらと多いです。
重みがゼロということは、そこの隠れ層のニューロンを無視していることになります。
せっかくニューロンを増やしたのに、使えるニューロンが３つしかないのなら、増やした意味が無いですよね。
TESTデータもこんな感じです。

（図6_05）

本来×と判定されなければいけないのに、先ほどと変わっていないですね。

これも多分、２章で述べたように、ソルバーが極小解なので、重み(W)のスタート地点が誤っていて、更に極小になるポイントがどこかにあるからだと思われます。
いろいろ難しいですね。

７．重みとバイアスのスタート位置を変え、更に小さい極小解を導いてみる

ニューロンを多くしても良い結果が得られない原因は、ソルバーが極小解しか導き出さず、最小解までたどり着けないからだと想像しました。

なら、重みとバイアスを手入力して、そこからソルバー再計算スタートさせてみたらどうなるのか実験してみます。

（図6_05）の平方誤差合計値(Qt)は、
13.49537741
でした。

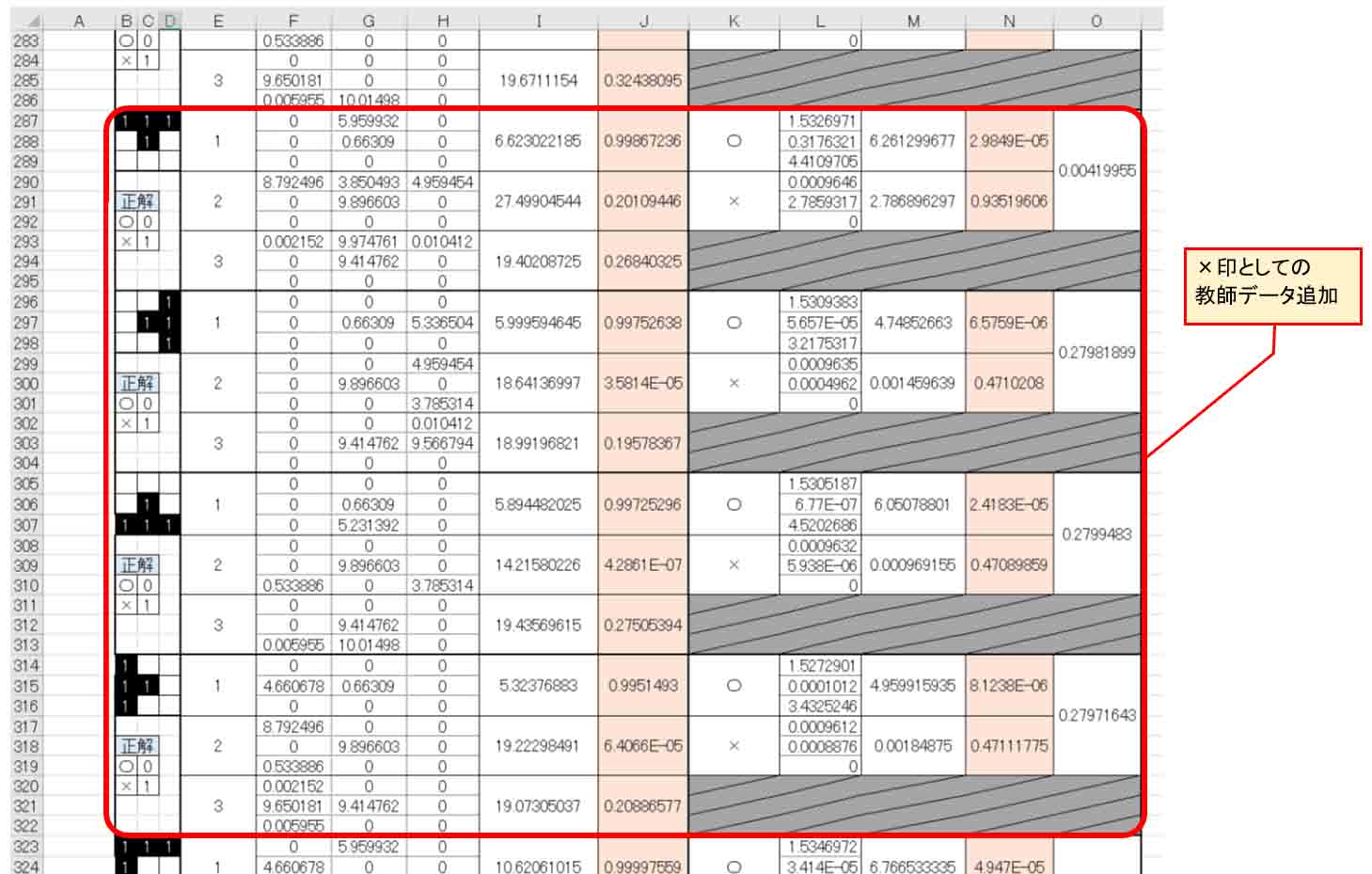
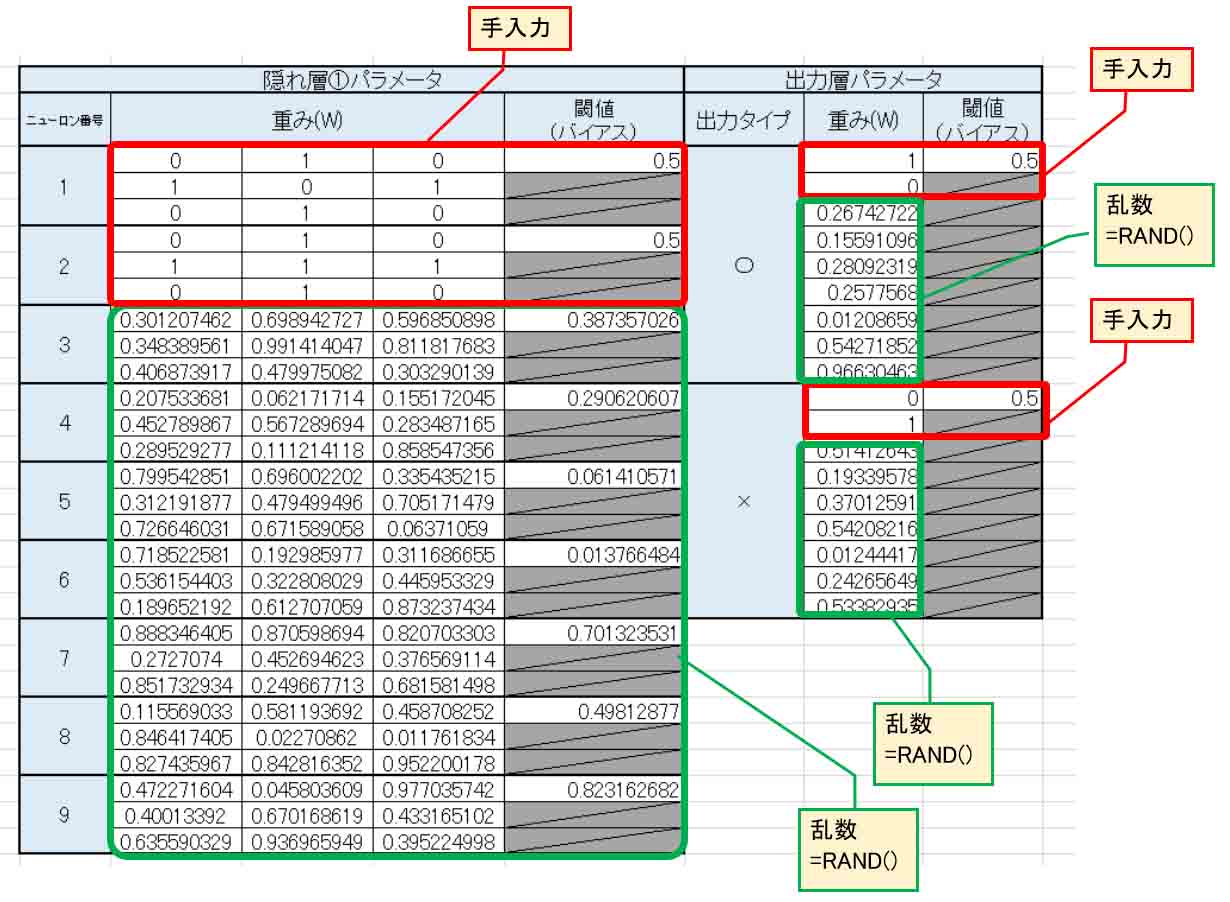
では、下図の様に重みとバイアス値の一部分を手入力して、他は全て乱数にしてみます。
これで正しく導き出されるかは分かりませんけど、とにかくやってみます。

（図7_01）

隠れ層①のニューロン１は、教師データから絶対○印なので、出力層の重みは○印で1とします。
一方、隠れ層①のニューロン２は絶対に×印なので、出力層の重みは×印で1とします。

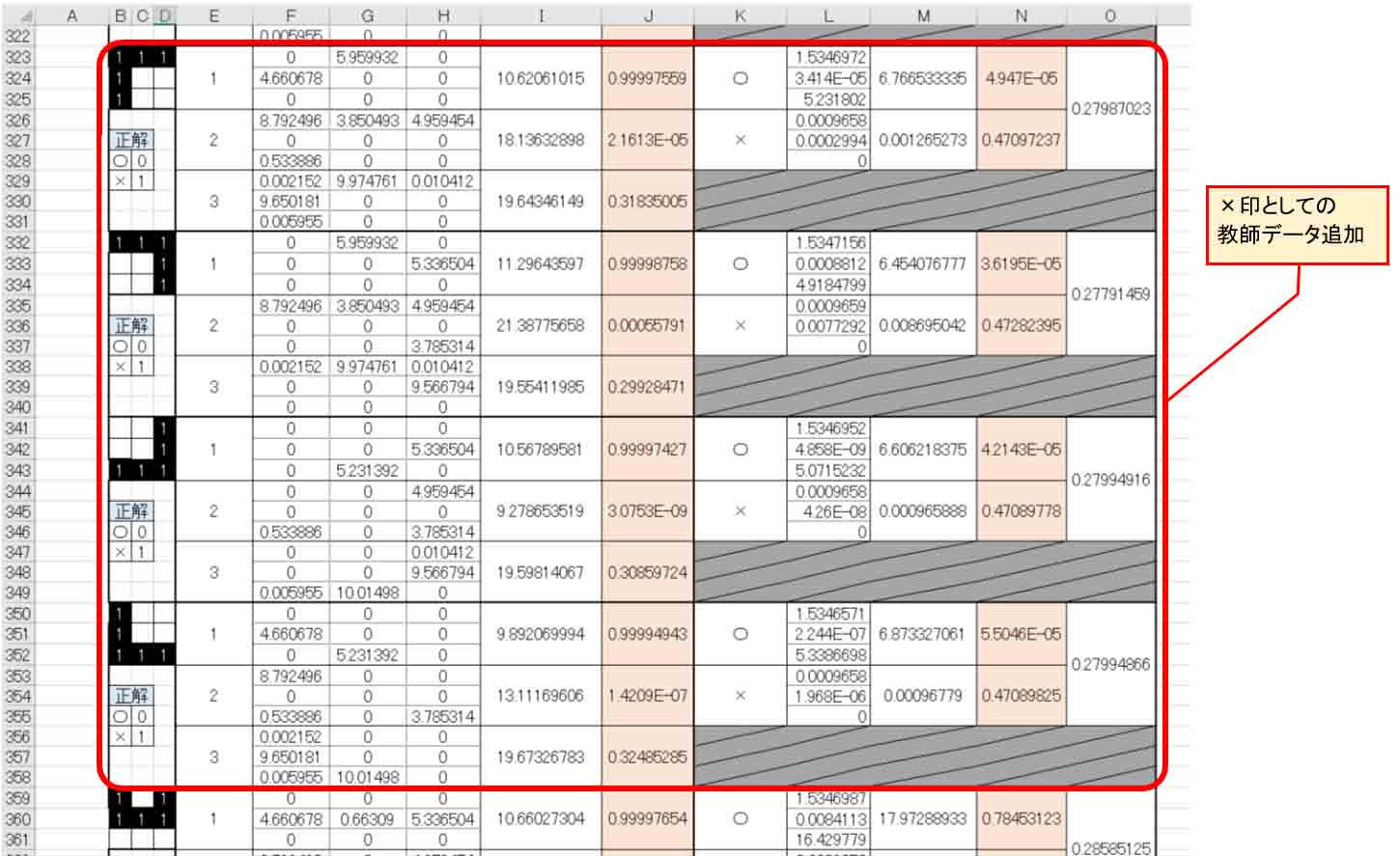
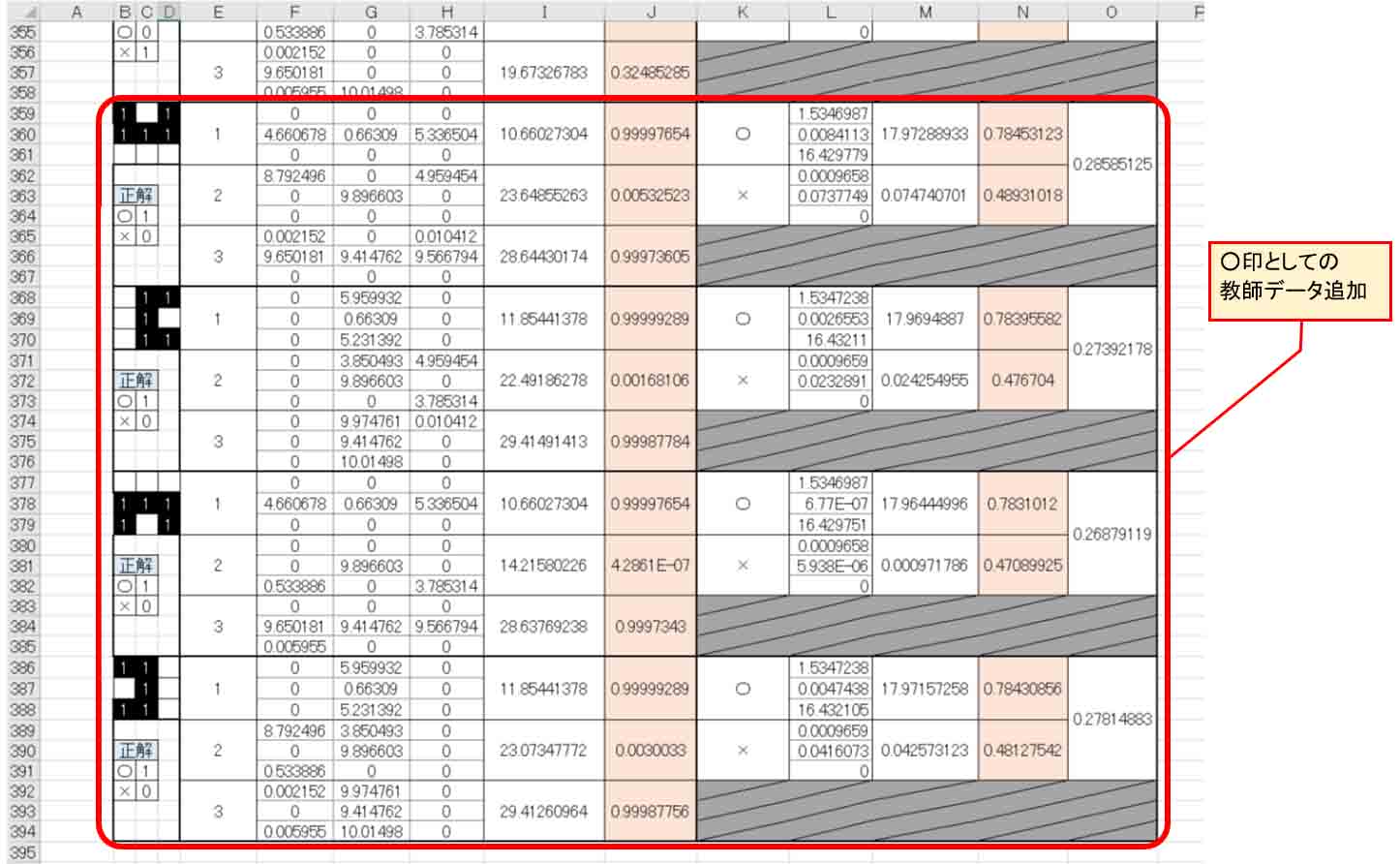
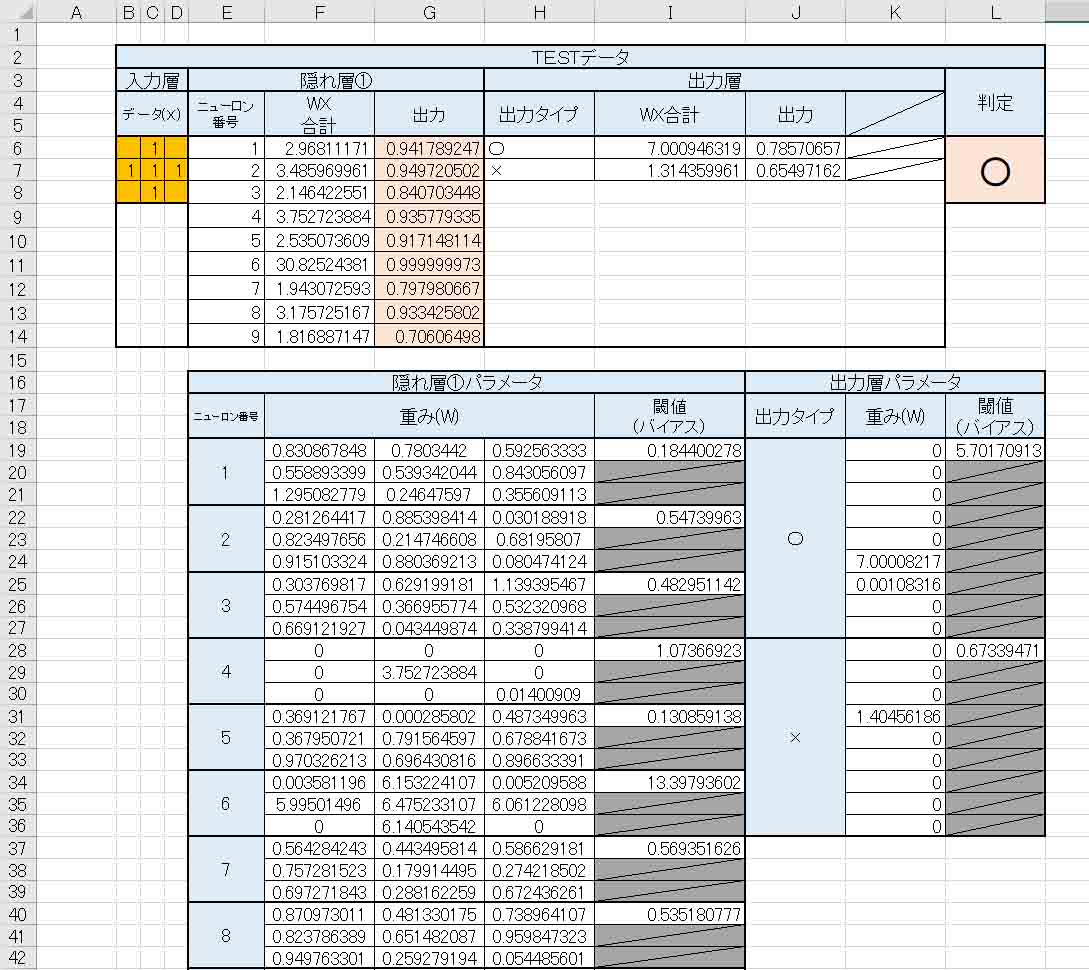
そして、ソルバーで極小解を計算させてみると、以下のような結果になりました。

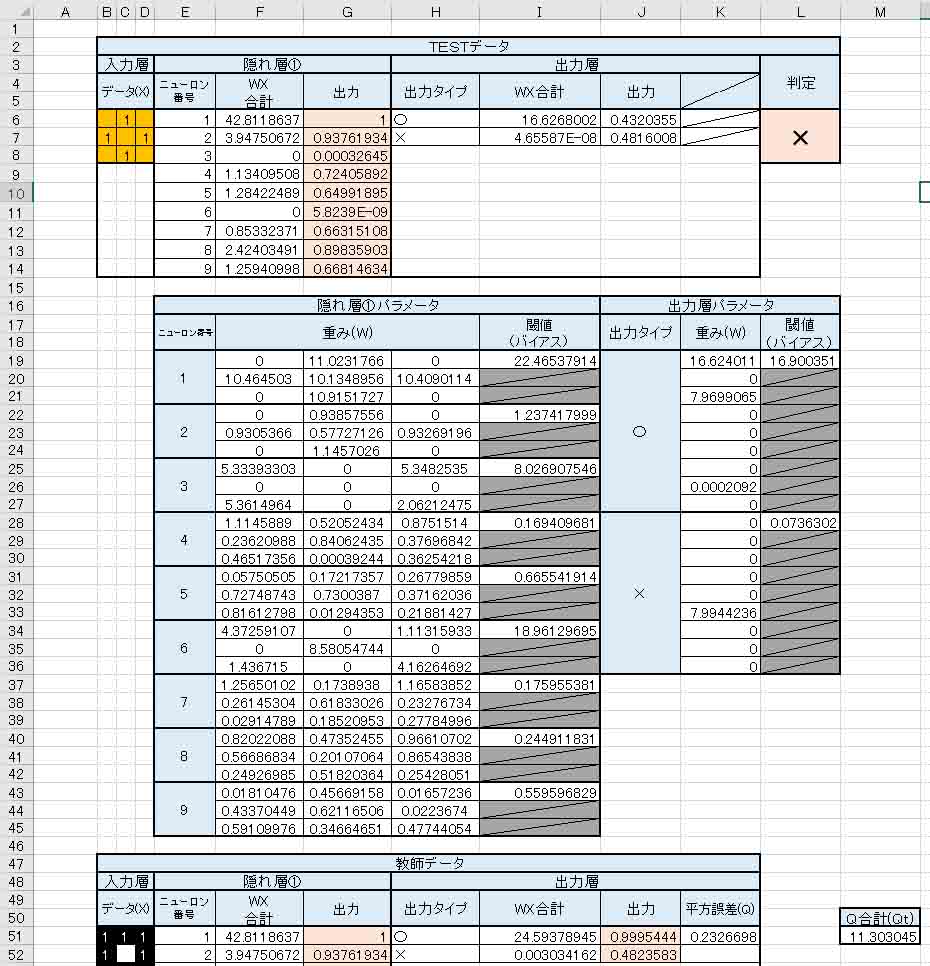
（図7_02）

右下端の平方誤差合計値(Qt)の値は、13.49537741から
11.30304462
となり、より小さくなりました。
そして、出力層の重み(W)は（図6_05）のときよりも○印のところがパラメータが一つ増えました。

しかし、肝心のTESTデータの判定は誤っています。
本来は○印として判定されなければなりません。

（図6_05）の時のTESTデータとは違うところで不正解になっていました。
結局、手入力もあまり効果無かったようです。

この後、何度も手入力してソルバーのスタート位置を変えてみました。
結果、Qtの値はより小さくなったのですが、肝心の判定結果は全問正解とはなりませんでした。

結局のところ、Excelのソルバーの最小値設定は、単なる極小値であって、重みやバイアスの初期値によって極小値が変化するということを頭に入れておかねばならないということが良く解りました。

では、全問正解にするにはどうしたらよいのか、次の実験をやってみます。

８．重みとバイアスに負の値を許容させたら、全問正解になった

ここまでの段階で、ニューロン９個の隠れ層１つのニューラルネットワークですが、これでも個人的にはきっと全問正解ができるはずだ、と睨んでいます。

参考書籍「Excelでわかるディープラーニング超入門」では、ソルバーの設定で、
「制約のない変数を非負数にする」
にチェックを入れると書いてありましたが、どうにも解決できなかったので、このチェックを外してみることにしました。
例のごとく、重み(W)とバイアス（閾値）は乱数を入力して初期値にします。

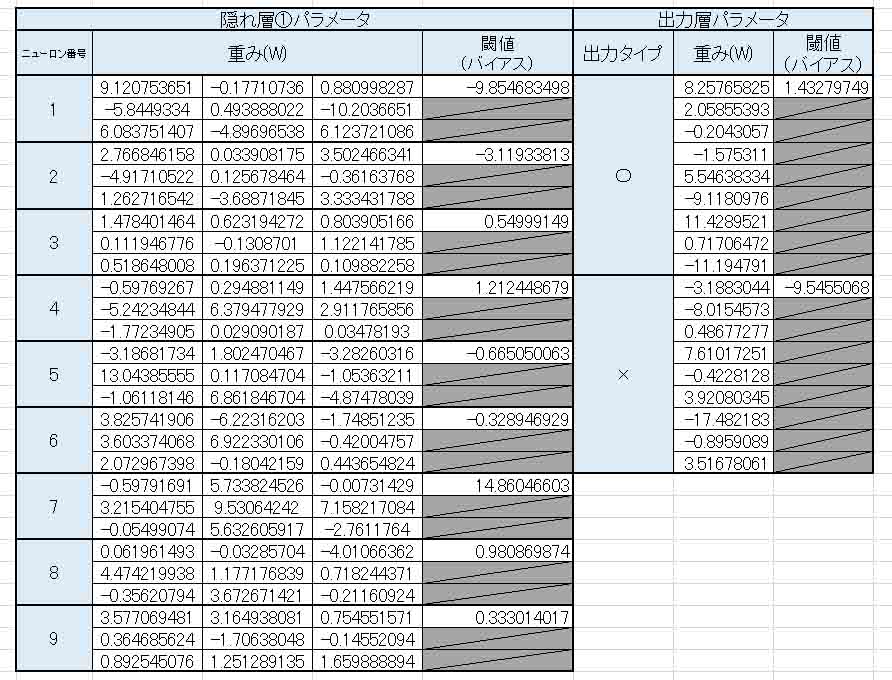
結果、以下のようになりました。

（図8_01）

以前と違って、重み(W)とバイアスに負の値が入っていて、出力層の重みもビッシリ値が入力されています。
そして、全ての値に0が無くなりました。
これは期待できそうです。

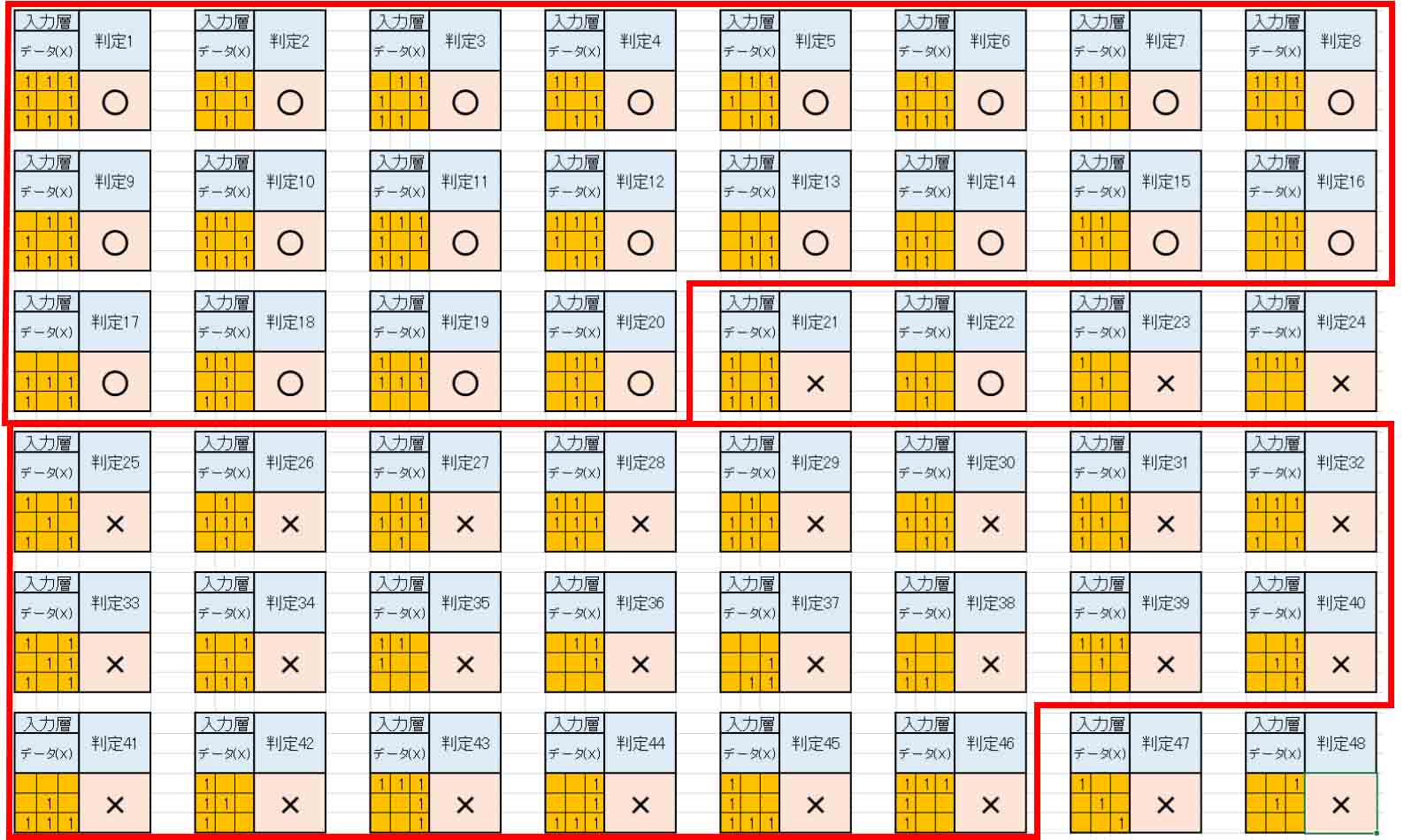
では、TESTデータの入力結果を見てみると、こんな感じになりました。

（図8_02）

赤枠内にあるものは、全て教師データにあるもので、なんと、全問正解しました。
ようやっとここまでたどり着けました。

さて、その他のデータを見てみると、判定21と判定23は○印になっていれば尚良いですね。

また、判定48は×印でＯＫなんですけど、判定47は何とも言えませんね。

でも、ここまで出来れば上出来です。

ただ、疑問が残るのは、重みやバイアスを負の値にして良いのかというところです。

最初に紹介した書籍「Excelでわかるディープラーニング超入門」では、生物界に負の値は存在しないから、全て正の値にすると書いてあるので、ちょっとスッキリしないですね。
ソルバー計算だから仕方ないのかも知れません。
この辺は良く解りません。

ゆくゆくはソルバーに頼らずに、自分自身でアルゴリズムを作って、最適解を導けるようにしたいと思います。

９．隠れ層を追加したら結果が良くなるのか？

重みとバイアスを正の値にするなら、隠れ層を一つ増やすと結果が良くなるのか？という実験をやってみます。

実験の前に想像するに、隠れ層①だけの状態でソルバー計算させても、出力層の重みがスカスカでゼロばかりだったので、隠れ層を増やしても効果無いだろうと思います。
でも、試しにやってみます。

まず、下図の様に隠れ層②を作って、ニューロンの数は３つにしておきます。
例のごとくすべての重みとバイアスには乱数を入力しておきます。

（図9_01）

次に、下図の様に教師データを修正しておきます。
教師データは先とおなじように４０パターンです。

（図9_02）

そうしたら、例のごとく、教師データをコピーしてTESTデータ欄を作成し、ソルバー設定で目的のセルを平方誤差合計(Qt)にし、変更セルを全重みと全バイアスにして、ソルバー解決します。

結果、下図のようになりました。

（図9_03）

出力層の重み(W)に0が多く、隠れ層②の意味が無いですね。

そして、TESTデータの判定も誤っています。
これは×印として判定されねばなりません。

ということで、隠れ層を一つ増やしても無駄でした。

これを８章のようにソルバー設定で負の値にしたとしても、イマイチうまくいきませんでした。
隠れ層を増やしても無駄だと事前にある程度わかっていたので、案の定という感じです。

以上から、むやみに隠れ層を増やしても意味が無いことが分かり、ソルバーの最適解も限界に達しました。

まぁ、そもそも、○印や×印が半分しか表現されていないものを正常に無理やり判定させる必要があるのかどうかというところも問題ですし、高解像度カメラならばたった9画素で判定させる必要は無いと思いますので、3x3 pixel の実験はこのくらいで止めておきます。

でも、IF文等の条件分岐無しで、似たような画素パターンでも図形の判別ができるようになったことは収穫でした。
これぞ、ニューラルネットワークとディープラーニングの醍醐味なのだろうと感じました。

まとめ

以上から、だんだんニューラルネットワークとディープラーニングの特徴が見えてきました。
また、ディープラーニングの一部を体感することができました。

特に、ソルバー学習で重みと閾値だけが自動的に割り当てられ、その数値で作ったニューラルネットワークの簡単な数式だけで正解を判定できるということは驚きです。
今までのプログラミングとは大きく異なりますね。
実際はソルバーのようなものを自作するときはプログラミングが必要ですが、ソルバーのようなユニットがあれば、ディープラーニングは全て自動で重みと閾値を与えてくれるということです。
ディープラーニングの肝はソルバーのような最適解を求めるアルゴリズムです。
これさえ自分で作ることができれば、ディープラーニングは自前で出来そうな気がしてきました。

また、ニューラルネットワークには、教師データの数によって隠れ層が必要になることが分かりました。

そして、教師データのパターン構成によって最初の隠れ層のニューロン数を決定すれば良いことが分かりました。
特に、出力の異なる類似した教師データが多くある場合はニューロンを相当分増やす必要がありそうです。

そして、隠れ層一つだけで概ねカバーできれば、隠れ層を増やす必要が無いことも分かりました。
出力層の重みに無駄なゼロ値がある場合は最適解とは程遠いということでした。

そして、ソルバーの注意点は極小解であって、最小解の最適解ではないということです。

今回分かったのはこんなところでしょうか。
いずれにしても以上はすべて自己流のド素人見解です。

だんだんディープラーニングとニューラルネットワークの挙動が見えてきた気がします。
それにしても、Excelでここまでできるとは驚きですね。
改めて、ここまでの考察がが得られるようになった参考書籍「Excelでわかるディープラーニング超入門」に感謝したいと思います。

今回はここまでで、次回は畳み込みニューラルネットワークをやってみたいと思います。

ではまた。。。

Amazon.co.jp 当ブログのおすすめ